(本小题共13分)为了解某地区中学生的身体发育状况,拟采用分层抽样的方法从甲、乙、丙三所中学抽取6个教学班进行调查.已知甲、乙、丙三所中学分别有12,6,18个教学班.
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数;
(Ⅱ)若从抽取的6个教学班中随机抽取2个进行调查结果的对比,求这2个教学班中至少有1个来自甲学校的概率.
如图所示,四棱锥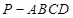 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,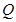 是棱
是棱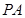 上的动点.
上的动点.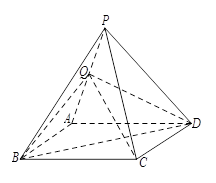
(1)若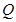 是
是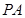 的中点,求证:
的中点,求证: //平面
//平面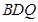 ;
;
(2)若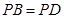 ,求证:
,求证: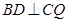 ;
;
(3)在(2)的条件下,若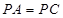 ,
,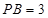 ,
,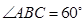 ,求四棱锥
,求四棱锥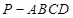 的体积.
的体积.
如图,平行四边形 中,
中,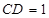 ,
,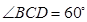 ,且
,且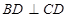 ,正方形
,正方形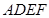 和平面
和平面 垂直,
垂直, 是
是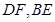 的中点.
的中点.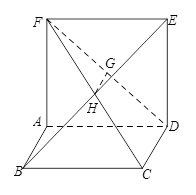
(1)求证: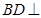 平面
平面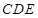 ;
;
(2)求证: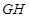 ∥平面
∥平面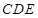 ;
;
(3)求三棱锥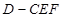 的体积.
的体积.
如图所示,ABCD是一块边长为100 m的正方形地皮,其中AST是一半径为90 m的扇形小山,其余部分都是平地.一开发商想在平地上建一个矩形停车场,使矩形的一个顶点P在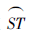 上,相邻两边CQ、CR落在正方形的边BC、CD上.求矩形停车场PQCR面积的最大值和最小值.
上,相邻两边CQ、CR落在正方形的边BC、CD上.求矩形停车场PQCR面积的最大值和最小值.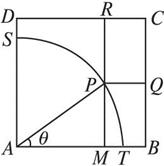
已知sin2θ(1+cotθ)+cos2θ(1+tanθ)=2,θ∈(0,2π),求tanθ的值.
已知△ABC的三个内角A、B、C,求当A为何值时,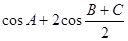 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.