如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0)。
(1)m为何值时,△OAB面积最大?最大值是多少?
(2)如图2,在(1)的条件下,函数 的图像与直线AB相交于C、D两点,若
的图像与直线AB相交于C、D两点,若 ,求k的值。
,求k的值。
(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10)。
2010年某市实现国民生产总值为986亿元.计划全市国民生产总值以后三年都以相同的增长率增长,并且2012年全市国民生产总值要达到1 l93.06亿元.求全市国民生产总值的年平均增长率。
先化简再求值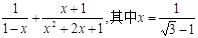 :
:
如图,抛物线 与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.
与x轴交于A、B两点,与y轴交于点C(0,-3)[图14(2)、图14(3)为解答备用图.
(1)k=_______,点A的坐标为___________,点C的坐标为_____________.
(2)设抛物线 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
已知,如图,在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得△GFC.
(1)求证:BE=DG;
(2)∠若B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论.
某电脑公司现有A、B、C三种型号的甲品牌电脑和D、E两种型号的乙品牌电脑,希望中学要从甲、乙两品牌电脑中各选一种型号的电脑。
(1)写出所有选购方案(利用树状图或列表法表示);
(2)如果(1)中各种选购方案被选中的可能性相同,那么A型号电脑被选中的概率是多少?
(3)现知希望中学购买甲、乙两种品牌电脑共36台(价格如右图所示),恰好用了10万元人民币,其中甲品牌电脑为A型电脑,求购买A型号电脑有几台?