如图，暑假快要到了，某市准备组织同学们分别到A，B，C，D四个地方进行夏令营活动，前往四个地方的人数．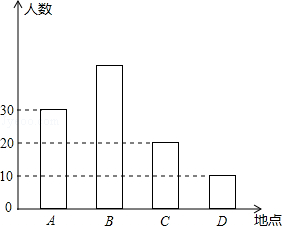
（1）去B地参加夏令营活动人数占总人数的40%，根据统计图求去B地的人数？
（2）若一对姐弟中只能有一人参加夏令营，姐弟俩提议让父亲决定．父亲说：现有4张卡片上分别写有1，2，3，4四个整数，先让姐姐随机地抽取一张后放回，再由弟弟随机地抽取一张．若抽取的两张卡片上的数字之和是5的倍数则姐姐参加，若抽取的两张卡片上的数字之和是3的倍数则弟弟参加．用列表法或树形图分析这种方法对姐弟俩是否公平？
为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家决定对购买彩电的农户实行政府补贴.规定每购买一台彩电，政府补贴若干元，经调查某家电商场销售彩电台数y（台）与补贴款额x（元）之间大致满足如图①所示的一次函数关系.随着补贴款额x的不断增大，销售量也不断增加，但每台彩电的收益Z（元）会相应降低且Z与x之间也大致满足如图②所示的一次函数关系.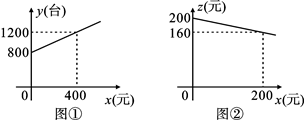
(1)在政府未出台补贴措施前，该商场销售彩电的总收益额为___________元.
(2)在政府补贴政策实施后，分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式；
(3)要使该商场销售彩电的总收益w（元）最大，政府应将每台补贴款额x定为多少并求出总收益w的最大值.
如图，在Rt△ABC中，∠C＝90°,∠ABC的平分线BD交AC于点D，DE⊥BD交AB于点E，设⊙O是△BDE的外接圆.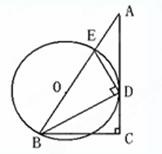
（1）求证：AC是⊙O的切线；
（2）求证：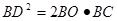
.
如图是某货站传送货物的平面示意图，AD与地面的夹角为60°，为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°变成37°，因此传送带的落地点由点B到点C向前移动了2米.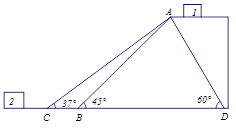
（1）求点A与地面的高度；
（2）如果需要在货物着地点C的左侧留出2米，那么请判断距离D点14米的货物2是否需要挪走，并说明理由.（sin37°≈0.6，cos37°≈0.8，tan37°≈0.75，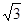
≈1.73）
某建设工程准备招标，指挥部现接到甲、乙两个工程队的投标书，从投标书中得知：乙队单独完成这项工程所需天数是甲队单独完成这项工程所需天数的2倍；该工程若由甲队先做6天，剩下的工程再由甲、乙两队合作16天可以完成.
（1）求甲、乙两队单独完成这项工程各需要多少天？
（2）已知甲队每天的施工费用为0.67万元，乙队每天的施工费用为0.33万元，该工程预算的施工费用为19万元.为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，问：该工程预算的施工费用是否够用？若不够用，需要追加预算多少万元？请说明理由.
如图，在直角梯形ABCD中，AD∥BC，AB⊥AD，BC＝CD，BE⊥CD，垂足为E，点F在BD上，连接AF、EF．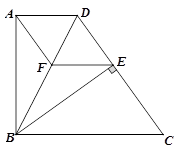
（1）求证：DA＝DE；
（2）如果AF∥CD，请判断四边形ADEF是什么特殊的四边形，并证明您的结论．