如图1所示，一张三角形纸片ABC，∠ACB＝90°，AC＝8，BC＝6．沿斜边AB的中线CD把这张纸片剪成△AC1D1和△BC2D2两个三角形(如图2所示)．将纸片△AC1D1沿直线D2B(AB)方向平移(点A，D1，D2，B始终在同一直线上)，当点D1与点B重合时，停止平移．在平移的过程中，C1D1与BC2交于点E，AC1与C2D2、BC2分别交于点F、P．当△AC1D1平移到如图3所示位置时，猜想D1E与D2F的数量关系，并说明理由
设平移距离D2D1为x，△AC1D1和△BC2D2重复部分面积为y，请写出y与x的函数关系式，以及自变量的取值范围；
对于(2)中的结论是否存在这样的x，使得重复部分面积等于原△ABC纸片面积的
？若存在，请求出x的值；若不存在，请说明理由．
图1 图2 图3
如图，已知△ABC中AB=AC．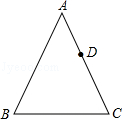
（1）作图：在AC上有一点D，延长BD，并在BD的延长线上取点E，使AE=AB，连AE，作∠EAC的平分线AF，AF交DE于点F（用尺规作图，保留作图痕迹，不写作法）；
（2）在（1）的条件下，连接CF，求证：∠E=∠ACF．
（1）计算：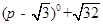
－8sin45°－
（2）先化简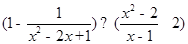
，然后x在﹣1、0、1、2四个数中任选一个合适的数代入求值．
如图，已知直线
分别交x轴、y轴于A、B两点，抛物线
经过A、B两点，点C是抛物线与x轴的另一个交点（与A点不重合）．
（1）求抛物线的解析式；
（2）求△ABC的面积；
（3）在抛物线的对称轴上，是否存在点M，使△ABM为等腰三角形？若不存在，请说明理由；若存在，求出点M的坐标．
如图1，正方形OABC与正方形ODEF放置在直线l上，连结AD、CF，此时AD=CF．AD⊥CF成立．
（1）正方形ODEF绕O点逆时针旋转一定的角度，如图2，试判断AD与CF还相等吗？若成立，请证明；若不成立，请说明理由．
（2）正方形ODEF绕O点逆时针旋转，使点E旋转至直线l上，如图3，求证：AD⊥CF．
（3）在（2）小题的条件下，AD与OC的交点为G，当AO=3，OD=
时，求线段CG的长．
如图，反比例函数
（x＞0）的图象经过线段OA的端点A，O为原点，作AB⊥x轴于点B，点B的坐标为（2，0），tan∠AOB=
．
（1）求k的值；
（2）将线段AB沿x轴正方向平移到线段DC的位置，反比例函数（x＞0）的图象恰好经过DC的中点E，求直线AE的函数表达式；
（3）若直线AE与x轴交于点M、与y轴交于点N，请你探索线段AN与线段ME的大小关系，写出你的结论并说明理由．