如图1,正方形OABC与正方形ODEF放置在直线l上,连结AD、CF,此时AD=CF.AD⊥CF成立.
(1)正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?若成立,请证明;若不成立,请说明理由.
(2)正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,求证:AD⊥CF.
(3)在(2)小题的条件下,AD与OC的交点为G,当AO=3,OD= 时,求线段CG的长.
时,求线段CG的长.
先化简,再求值: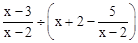 ,其中
,其中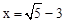 .
.
如图,在平面直角坐标系中,顶点为(3,4)的抛物线交 y轴与A点,交x轴与B、C两点(点B在点C的左侧),已知A点坐标为(0,-5).
(1)求此抛物线的解析式;
(2)过点B作线段AB的垂线交抛物线与点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C的位置关系,并给出证明.
(3)在抛物线上是否存在一点P,使△ACP是以AC为直角边的直角三角形.若存在,求点P的坐标;若不存在,请说明理由.
周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.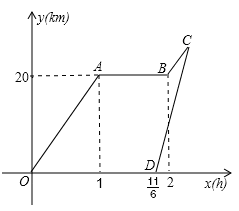
(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.
阅读下面的材料,先完成阅读填空,再将要求答题: ,则
,则 ;①
;①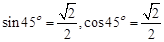 ,则
,则 ; ②
; ② ,则
,则 . ③
. ③
……
观察上述等式,猜想:对任意锐角A,都有 .④
.④
(1)如图,在锐角三角形ABC中,利用三角函数的定义及勾股定理对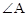 证明你的猜想;
证明你的猜想;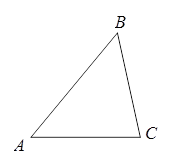
(2)已知: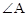 为锐角
为锐角 且
且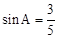 ,求
,求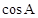 .
.
如图,已知AB是⊙O的直径,P为⊙O外一点,且OP∥BC,∠P=∠BAC .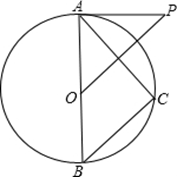
(1)求证:PA为⊙O 的切线;
(2)若OB=5,OP=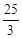 ,求AC的长.
,求AC的长.