如图，在平面直角坐标系中，顶点为（3，4）的抛物线交 y轴与A点，交x轴与B、C两点（点B在点C的左侧），已知A点坐标为（0，－5）．
（1）求此抛物线的解析式；
（2）过点B作线段AB的垂线交抛物线与点D，如果以点C为圆心的圆与直线BD相切，请判断抛物线的对称轴与⊙C的位置关系，并给出证明．
（3）在抛物线上是否存在一点P，使△ACP是以AC为直角边的直角三角形．若存在，求点P的坐标；若不存在，请说明理由．
某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．
（1）求该校八年级学生参加社会实践活动的人数；
（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．请你计算本次社会实践活动所需车辆的租金．
如图，在△ABC中，D是BC边的中点，E、F分别在AD及其延长线上， CE∥BF，连接BE、CF．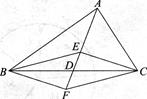
（1）求证：△BDF≌△CDE；
（2）当△ABC满足什么条件时，四边形BFCE是菱形？
进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话:
通过这段对话,请你求出该地驻军原来每天加固的米数.
如图，已知抛物线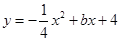
与x轴相交于A、B两点，与y轴相交于点C，若已知B点的坐标为B（8，0）．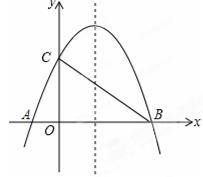
（1）求抛物线的解析式及其对称轴方程；
（2）连接AC、BC，试判断△AOC与△COB是否相似？并说明理由；
（3）M为抛物线上BC之间的一点，N为线段BC上的一点，若MN∥y轴，求MN的最大值；
（4）在抛物线的对称轴上是否存在点Q，使△ACQ为等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
已知：Rt△ABC和Rt△DBE，AB=BC，DB=EB，D在AB上，连接AE，AC，如图1延长CD交AE于k．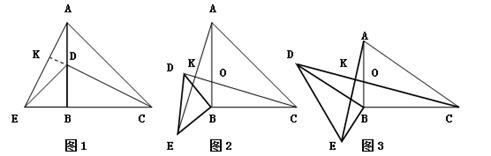
（1）求证：AE＝CD，AE⊥CD；
（2）类比：如图2所示，将（1）中的Rt△DBE绕点B逆时针旋转一个锐角，问（1）中线段AE，CD之间数量关系和位置关系还成立吗？若成立，请给予证明；若不成立，请说明理由；
（3）拓展：在图2中，将“AB=BC，DB=EB”改为“AB=kBC，DB=kEB，k>1”其它条件均不变，如图3所示，问（1）中线段AE，CD间的数量关系和位置关系怎样？请直接写出线段AE，CD间的数量关系和位置关系．