已知:Rt△ABC和Rt△DBE,AB=BC,DB=EB,D在AB上,连接AE,AC,如图1延长CD交AE于k.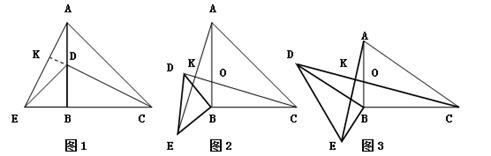
(1)求证:AE=CD,AE⊥CD;
(2)类比:如图2所示,将(1)中的Rt△DBE绕点B逆时针旋转一个锐角,问(1)中线段AE,CD之间数量关系和位置关系还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)拓展:在图2中,将“AB=BC,DB=EB”改为“AB=kBC,DB=kEB,k>1”其它条件均不变,如图3所示,问(1)中线段AE,CD间的数量关系和位置关系怎样?请直接写出线段AE,CD间的数量关系和位置关系.
已知抛物线 的顶点在抛物线
的顶点在抛物线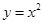 上,且抛物线在
上,且抛物线在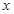 轴上截得的线段长是
轴上截得的线段长是 ,求
,求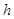 和
和 的值.
的值.
下表给出了代数式 与
与 的一些对应值:
的一些对应值:
 |
… |
0 |
1 |
2 |
3 |
4 |
… |
 |
… |
3 |
 |
3 |
… |
(1)请在表内的空格中填入适当的数;
(2)设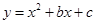 ,则当
,则当 取何值时,
取何值时,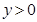 ?
?
(3)请说明经过怎样平移函数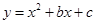 的图象得到函数
的图象得到函数 的图象.
的图象.
抛物线
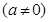 过点
过点 ,顶点为M点.
,顶点为M点.
(1)求该抛物线的解析式;
(2)试判断抛物线上是否存在一点P,使∠POM=90˚.若不存在,说明理由;若存在,求出P点的坐标;
(3)试判断抛物线上是否存在一点K,使∠OMK=90˚,说明理由.
如图,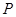 为抛物线
为抛物线 上对称轴右侧的一点,且点
上对称轴右侧的一点,且点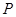 在
在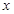 轴上方,过点
轴上方,过点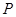 作
作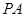 垂直
垂直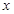 轴于点
轴于点 ,
,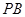 垂直
垂直 轴于点
轴于点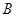 ,得到矩形
,得到矩形 .若
.若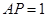 ,求矩形
,求矩形 的面积.
的面积.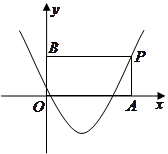
如图,已知抛物线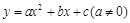 经过
经过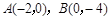 ,
,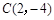 三点,且与
三点,且与 轴的另一个交点为
轴的另一个交点为 .
.
(1)求抛物线的解析式;
(2)用配方法求抛物线的顶点 的坐标和对称轴;
的坐标和对称轴;
(3)求四边形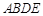 的面积.
的面积.