如图,已知抛物线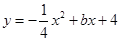 与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).
与x轴相交于A、B两点,与y轴相交于点C,若已知B点的坐标为B(8,0).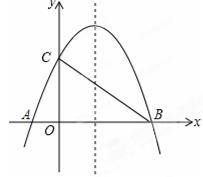
(1)求抛物线的解析式及其对称轴方程;
(2)连接AC、BC,试判断△AOC与△COB是否相似?并说明理由;
(3)M为抛物线上BC之间的一点,N为线段BC上的一点,若MN∥y轴,求MN的最大值;
(4)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.
如图,在平面直角坐标系中,直线y=-x-3与抛物线y=x2+mx+n相交于两个不同的点A、B,其中点A在x轴上.
(1)则A点坐标为;
(2)若点B为该抛物线的顶点,求m、n的值;
(3)在(2)条件下,设该抛物线与x轴的另一个交点为C,请你探索在平面内是否存在点D,使得△DAC与△DCO相似?如果存在,求出点D的坐标;如果不存在,请说明理由.
如图,在△ABC中,∠BCA=90°,以BC为直径的⊙O交AB于点P,Q是AC的中点,连接QP并延长交CB的延长线于点D.
(1)判断直线PQ与⊙O的位置关系,并说明理由:
(2)若AP=4,tanA=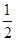 ,
,
①求⊙O的半径的长;
②求PD的长.
某水果店出售一种水果,每只定价20元时,每周可卖出300只.试销发现:
(1)每只水果每降价1元,每周可多卖出25只.设现在定价每只x元(x<20),一周销售收入为y元,则y与x的函数关系式为;
(2)每只水果每涨价1元,每周将少卖出10只,如何定价,才能使一周销售收入最多?
(3)根据以上信息,你认为应当如何定价才能使一周销售收入最多?
如图,在⊙O的内接四边形ABCD中,AB=AD,∠C=120°,点E在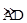 上.
上.
(1)求∠E的度数;
(2)连接OD、OE,当∠DOE=90°时,AE恰好为⊙O的内接正n边形的一边,求n的值.
已知关于x的方程x2-(k+1)x+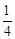 k2+1=0.
k2+1=0.
(1)若方程有两个不相等的实数根,求k的取值范围;
(2)若方程的两根恰好是一个矩形两邻边的长,且k=4,求该矩形的对角线的长.