已知:正方形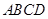 的边长为1,射线
的边长为1,射线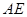 与射线
与射线 交于点
交于点 ,射线
,射线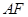 与射线
与射线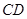 交于点
交于点 ,
, .
.
(1)如图1,当点 在线段
在线段 上时,试猜想线段
上时,试猜想线段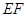 、
、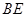 、
、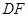 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想.
(2)设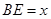 ,
,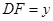 ,当点
,当点 在线段
在线段 上运动时(不包括点
上运动时(不包括点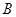 、
、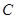 ),如图1,求
),如图1,求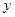 关于
关于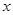 的函数解析式,并指出
的函数解析式,并指出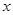 的取值范围.
的取值范围.
(3)当点 在射线
在射线 上运动时(不含端点
上运动时(不含端点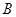 ),点
),点 在射线
在射线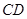 上运动.试判断以
上运动.试判断以 为圆心以
为圆心以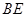 为半径的
为半径的 和以
和以 为圆心以
为圆心以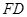 为半径的
为半径的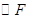 之间的位置关系.
之间的位置关系.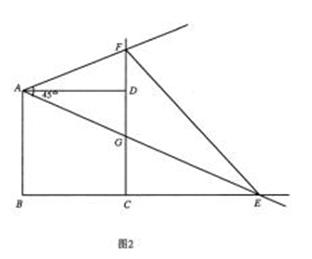
(4)当点 在
在 延长线上时,设
延长线上时,设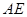 与
与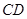 交于点
交于点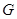 ,如图2.问△
,如图2.问△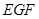 与△
与△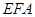 能否相似,若能相似,求出
能否相似,若能相似,求出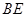 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.
在平面直角坐标系中,已知抛物线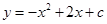 过点
过点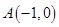 ;直线
;直线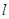 :
: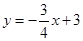 与
与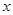 轴交于点
轴交于点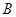 ,与
,与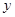 轴交于点
轴交于点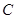 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点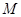 ;抛物线的顶点为
;抛物线的顶点为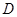 .
.
(1)求抛物线的解析式及顶点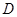 的坐标;
的坐标;
(2)过点 作
作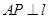 于点
于点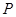 ,
,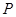 为垂足,求点
为垂足,求点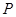 的坐标.
的坐标.
(3)若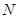 为直线
为直线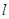 上一动点,过点
上一动点,过点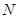 作
作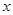 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点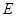 .问:是否存在这样的点
.问:是否存在这样的点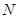 ,使得点
,使得点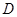 、
、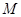 、
、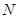 、
、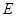 为顶点的四边形为平行四边形?若存在,求出点
为顶点的四边形为平行四边形?若存在,求出点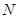 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
如图,在梯形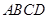 中,
中,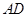 ∥
∥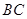 ,
,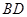 平分
平分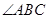 ,
,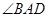 平分线交
平分线交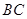 于
于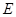 ,联结
,联结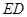 .
.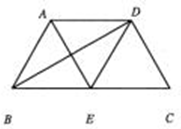
(1)求证:四边形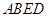 是菱形;
是菱形;
(2)当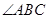 =60°,
=60°,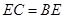 时,证明:梯形
时,证明:梯形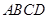 是等腰梯形.
是等腰梯形.
从2011年5月1日起,我市公安部门加大了对“酒后驾车”的处罚力度,出台了不准酒后驾车的禁令.某记者在某区随机选取了几个停车场对开车的司机进行了相关的调查,本次调查结果有四种情况: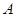 .有酒后开车;
.有酒后开车; .喝酒后不开车或请专业司机代驾;
.喝酒后不开车或请专业司机代驾; .开 车当天不喝酒;
.开 车当天不喝酒; .从不喝酒.将这次调查情况整理并绘制了如下尚不完整的统计图一和图二,请根据相关信息,解答下列问题.
.从不喝酒.将这次调查情况整理并绘制了如下尚不完整的统计图一和图二,请根据相关信息,解答下列问题.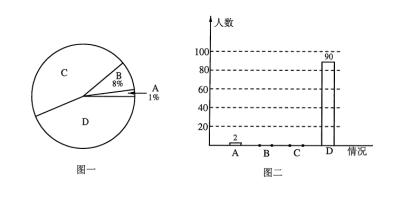
(1)该记者本次一共调查了名司机;
(2)图一中的情况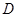 所在扇形的圆心角为______°;
所在扇形的圆心角为______°;
(3)补全图二;
(4)在本次调查中,记者随机采访其中的一名司机,则他属于情况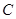 的概率是;
的概率是;
(5)若该区有3万名司机,则其中不违反“酒驾”禁令的人数约为人.
已知:如图,点点 、
、 分别在线段
分别在线段 、
、 上,
上, .
.
(1)求证:△ ∽△
∽△ ;
;
(2) ,
, ,
, ,求
,求 .
.