已知:正方形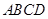 的边长为1,射线
的边长为1,射线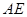 与射线
与射线 交于点
交于点 ,射线
,射线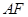 与射线
与射线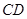 交于点
交于点 ,
, .
.
(1)如图1,当点 在线段
在线段 上时,试猜想线段
上时,试猜想线段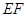 、
、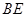 、
、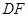 有怎样的数量关系?并证明你的猜想.
有怎样的数量关系?并证明你的猜想.
(2)设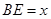 ,
,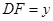 ,当点
,当点 在线段
在线段 上运动时(不包括点
上运动时(不包括点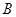 、
、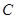 ),如图1,求
),如图1,求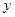 关于
关于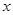 的函数解析式,并指出
的函数解析式,并指出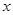 的取值范围.
的取值范围.
(3)当点 在射线
在射线 上运动时(不含端点
上运动时(不含端点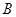 ),点
),点 在射线
在射线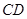 上运动.试判断以
上运动.试判断以 为圆心以
为圆心以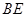 为半径的
为半径的 和以
和以 为圆心以
为圆心以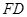 为半径的
为半径的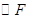 之间的位置关系.
之间的位置关系.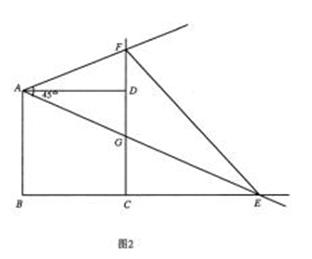
(4)当点 在
在 延长线上时,设
延长线上时,设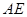 与
与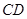 交于点
交于点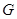 ,如图2.问△
,如图2.问△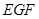 与△
与△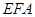 能否相似,若能相似,求出
能否相似,若能相似,求出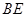 的值,若不可能相似,请说明理由.
的值,若不可能相似,请说明理由.
在刚刚过去的国庆假期中,全国高速公路免费通行,各地景区游人如织.在昆明世博园景区游客甚至“攻陷”了售票处,10月1日的游客人数约为3.9万人,接下来的六天中,每天的游客人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数). (1)10月3日的人数为多少万人?
(1)10月3日的人数为多少万人?
(2)七天假期里,游客人数最多的是10月几日,达到几万人?游客人数最少的是10月几日,达到几万人?
(3)请问昆明世博园景区在这七天内一共接待了多少游客?(结果精确到万位)
(4)如果你全家也打算出游昆明世博园景区,对出行的时间有何建议?
某巡警骑摩托车在一条南北大道上巡逻.某天他从岗亭出发,晚上停留在A处.规定向北方向为正.当天行驶记录如下(单位:千米).
+10,﹣8,+6,﹣13,+7,﹣12,+3,﹣2
①该巡警巡逻时离岗亭最远是多少千米?
②在岗亭北面6千米处有个加油站,该巡警巡逻时经过加油站几次?
③A在岗亭何方距岗亭多远?
④若摩托车每行1千米耗油0.05升,那么该摩托车这天巡逻共耗油多少升?
已知a,b互为相反数,c,d互为倒数,x的绝对值是2,且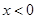 ,求
,求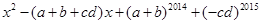 的值.
的值.
在数轴上标出下列各数:-1.5,2,+(-1),0,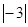 并用“<”连接起来.
并用“<”连接起来.
如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG。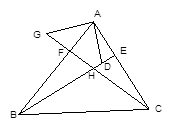
求证:(1)AD=AG,(2)AD与AG的位置关系如何?