某巡警骑摩托车在一条南北大道上巡逻．某天他从岗亭出发，晚上停留在A处．规定向北方向为正．当天行驶记录如下（单位：千米）．
+10，﹣8，+6，﹣13，+7，﹣12，+3，﹣2
①该巡警巡逻时离岗亭最远是多少千米？
②在岗亭北面6千米处有个加油站，该巡警巡逻时经过加油站几次？
③A在岗亭何方距岗亭多远？
④若摩托车每行1千米耗油0.05升，那么该摩托车这天巡逻共耗油多少升？
解方程（组）：（1）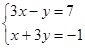
（2）
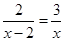
（3）x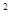
－2x＝2x＋1；
（4）x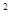﹣3x=0
（5）
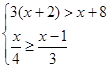
如图，直线l经过点A（1，0），且与双曲线y＝
（x＞0）交于点B（2，1），过点P（p，p－1）（p＞1）作x轴的平行线分别交曲线y＝（x＞0）和y＝－（x＜0）于M，N两点．
（1）求m的值及直线l的解析式；
（2）若点P在直线y＝2上，求证：△PMB∽△PNA；
（3）是否存在实数p，使得S△AMN＝4S△APM？若存在，请求出所有满足条件的p的值；若不存在，请说明理由．
如图，一次函数y1＝x＋1的图象与反比例函数y2＝
（k为常数，且k≠0）的图象都经过点
A（m，2）．
（1）求点A的坐标及反比例函数的表达式；
（2）结合图象直接比较：当x＞0时，y1与y2的大小．
如图，已知A（4，a），B（－2，－4）是一次函数y＝kx＋b的图象和反比例函数
的图象的交点．
（1）求反比例函数和一次函数的解析式；
（2）求△AOB的面积．
已知直线
经过点P（
，
），点P关于
轴的对称点P′在反比例函数
（
）的图象上．
（1）求的值；
（2）直接写出点P′的坐标；
（3）求反比例函数的解析式．