在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.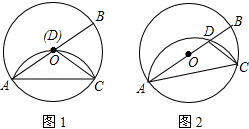
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
如图,在△ABC中,点D、E分别是边BC、AC的中点,过点A作AF∥BC交DE的延长线于F点,连接AD、CF.当△ABC满足什么条件时,四边形ADCF是菱形?为什么?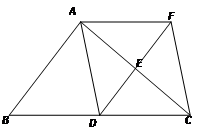
某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的莆田——我最喜爱的莆田美食”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图

请根据所给信息解答以下问题: (1)请补全条形统计图;
(1)请补全条形统计图;
(2)若全校有2000名同学,请估计全校同学中最喜爱“扁食”的同学有多少人;
(3)在一个不透明的口袋中有四个完全相同的小球,把它们分别标号为四种小吃的序号A、B、C、D,随机地摸出一个小球然后放回,再随机地摸出一个小球,请用列表或画树形图的方法,求出恰好两次都摸到“A”的概率。
解方程: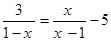 .
.
如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点O,根据下列条件,求出∠BOC的度数.
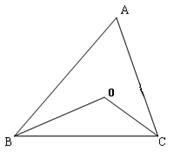
(1)已知∠ABC+∠ACB=100°,则∠BOC= .
(2)已知∠A=90°,求∠BOC的度数.
(3)从上述计算中,你能发现∠BOC与∠A的关系吗?请直接写出∠B0C与∠A的关系.
小华骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与离家距离的关系示意图.根据图中提供的信息回答下列问题: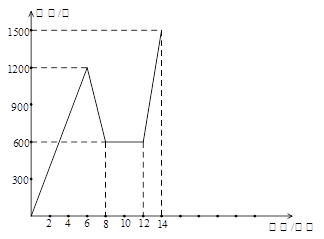
(1)小华家到学校的路程是多少米?
(2)在整个上学的途中哪个时间段小华骑车速度最快,最快的速度是多少米/分?
(3)小华在书店停留了多少分钟?
(4)本次上学途中,小华一共行驶了多少米?
(5)如果小华到校后立刻以300米/分的匀速度回家,请在原图上画出小华回家所用时间与离家距离的关系图象.