如图所示,MPQ为竖直面内一固定轨道,MP是半径为R的1/4光滑圆弧轨道,它与水平轨道PQ相切于P,Q端固定一竖直挡板,PQ长为s。一质量为m的小物块在M端由静止开始沿轨道下滑,与挡板发生一次碰撞(碰撞无机械能损失)后停在距Q点为L的地方,重力加速度为g,不计空气阻力。求:
(1)物块滑至圆弧轨道P点时轨道对物块的支持力大小;
(2)物块与PQ段动摩擦因数μ。
如图6-2-13所示,有一质量为m,带电荷量为+q的小球(可视为质点),自竖直向下、场强为E的匀强电场中的P点静止下落.在距离P点正下方h处有一弹性绝缘挡板S(挡板不影响匀强电场的分布),小球每次与挡板S相碰后电荷量均减少到碰前的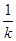 (k>1),而碰撞过程中小球的机械能不发生损失.
(k>1),而碰撞过程中小球的机械能不发生损失.
图6-2-13
(1)设匀强电场中,挡板S处电势φS=0,则电场中P点的电势φP为多少?小球在P点时的电势能EP为多少?
(2)小球从P点出发后到第一次速度变为零的过程中电场力对小球做了多少功?
(3)求在以后的运动过程中,小球距离挡板的最大距离l.
如图6-1-18所示,绝缘水平面上静止着两个质量均为m、电量均为+Q的物体A和B(A、B均可视为质点),它们间的距离为r,与水平面间的动摩擦因数均为μ.求:
图6-1-18
(1)A受到的摩擦力.
(2)如果将A的电量增至+4Q,则两物体将开始运动,当它们的加速度第一次为零时,A、B各运动了多远的距离?
如图5-4-6,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.
图5-4-6
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其他星球的影响.可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为T2.已知地球和月球的质量分别为5.98×1024 kg和7.35×1022 kg.求T2与T1两者平方之比.(结果保留3位小数)
在用高级沥青铺设的高速公路上,汽车的设计时速是108 km/h.汽车在这种路面上行驶时,它的轮胎与地面的最大静摩擦力等于车重的0.6倍.(取g=10 m/s2)
(1)如果汽车在这种高速路的水平弯道上拐弯,假设弯道的路面是水平的,拐弯时不产生横向滑动,其弯道的最小半径是多少?
(2)如果高速路上设计了圆弧形拱桥做立交桥,要使汽车能够不离开地面安全通过圆弧拱桥,这个圆弧拱桥的半径应满足什么条件?
如图5-1-14甲所示,在一端封闭、长约1 m的玻璃管内注满清水,水中放置一个蜡块,将玻璃管的开口端用胶塞塞紧.然后将这个玻璃管倒置,在蜡块沿玻璃管上升的同时,将玻璃管水平向右移动.假设从某时刻开始计时,蜡块在玻璃管内每1 s上升的距离都是10 cm,玻璃管向右匀加速平移,每1 s通过的水平位移依次是2.5 cm、7.5 cm、12.5 cm、17.5 cm.图乙中,y表示蜡块竖直方向的位移,x表示蜡块随玻璃管运动的水平位移,t=0时蜡块位于坐标原点.
图5-1-14
(1)请在图乙中画出蜡块4 s内的运动轨迹.
(2)求出玻璃管向右平移的加速度.
(3)求t=2 s时蜡块的速度v.