求函数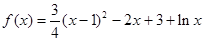
在区间[1,3]上的极值。
已知直线
为曲线
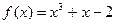在点（1，0）处的切线，直线
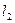为该曲线的另一条切线，且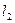的斜率为1。
（Ⅰ）求直线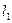
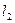、的方程；
（Ⅱ）求由直线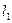、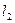和x轴所围成的三角形面积。
已知
，设P：函数
在R上递增，Q：关于x的不等式
对
恒成立.如果P且Q为假，P或Q为真，求
的取值范围
已知集合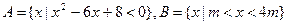
,
（Ⅰ）若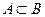
，求实数m的取值范围；
（Ⅱ）是否存在m使得A∪B=A？若有请求出m的范围，若无则说明理由。
（共2小题做答，每小题7分）
1．（选修4—2矩阵与变换）
变换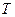
是将平面上每个点
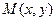的横坐标乘2，纵坐标乘4，变到点
。
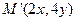（1）求变换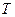的矩阵；
（2）圆
在变换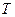的作用下变成了什么图形？
（本小题满分14分）已知函数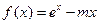
（1）当m=1时,求函数f(x)的最小值；
（2）若函数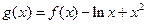
存在两个零点,求m的取值范围；
（3）证明:
。