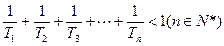(1)解不等式
(2)求函数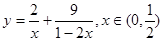 的最小值
的最小值
(本题满分12分)有人预测:在2010年的广州亚运会上,排球赛决赛将在中国队与日本队之间展开,据以往统计, 中国队在每局比赛中胜日本队的概率为 ,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.(Ⅰ)求中国队以3:1获胜的概率;(Ⅱ)设
,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛.(Ⅰ)求中国队以3:1获胜的概率;(Ⅱ)设 表示比赛的局数,求
表示比赛的局数,求 的期望值.
的期望值.
(本题满分12分)在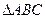 中,
中,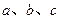 为角
为角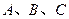 所对的三边,已知
所对的三边,已知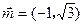 ,
, ,
, .(Ⅰ)求角
.(Ⅰ)求角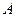 ;(Ⅱ)若
;(Ⅱ)若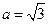 ,设
,设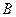 =
=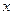 ,
,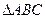 的周长为
的周长为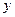 ,求
,求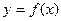 的最大值.
的最大值.
已知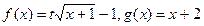 ,(
,(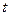 为参数)(1)当
为参数)(1)当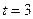 时,解不等式
时,解不等式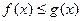 (2)如果当
(2)如果当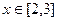 时,
时,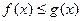 恒成立,求
恒成立,求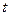 的取值范围。
的取值范围。
(满分13分)已知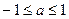 ,若
,若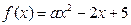 在区间
在区间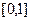 上的最小值为
上的最小值为 ,求
,求 的值。
的值。
(本小题满分13分)已知等比数列 的公比为
的公比为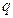 ,前
,前 项和为
项和为 ,且
,且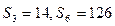 ,现若以
,现若以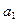 为首项
为首项 ,以公比
,以公比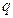 作为公差d构造新的等差数列
作为公差d构造新的等差数列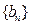
(1)求通项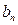 (2)记
(2)记 ,证明
,证明