在半径为4的⊙O中,点C是以AB为直径的半圆的中点,OD⊥AC,垂足为D,点E是射线AB上的任意一点,DF//AB,DF与CE相交于点F,设EF= ,DF=
,DF= .
. 

(1) 如图1,当点E在射线OB上时,求 关于
关于 的函数解析式,并写出自变量
的函数解析式,并写出自变量 的取值范围;
的取值范围;
(2) 如图2,当点F在⊙O上时,求线段DF的长;
(3) 如果以点E为圆心、EF为半径的圆与⊙O相切,求线段DF的长.
如图,已知一次函数y=kx+b(k≠0)的图象与反比例函数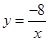 的图象交于A,B两点,且A点的横坐标与B点的纵坐标都是
的图象交于A,B两点,且A点的横坐标与B点的纵坐标都是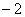 ;求:
;求: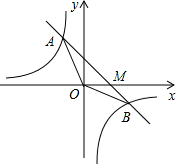
(1)一次函数的解析式;
(2)根据图像回答,当一次函数的值大于反比例函数的值时,写出x的取值范围;
(3)求 △AOB的面积。
如图,等腰△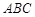 中,
中,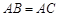 ,D是BC上一点,且
,D是BC上一点,且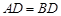 .
.
(1)求证:△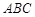 ∽△
∽△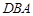 ;
;
(2)若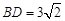 ,
,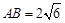 ,求
,求 的长;
的长;
(3)若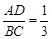 ,求
,求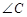 的度数.
的度数.
如图,某船由西向东航行,在点A测得小岛O在北偏东60°,船航行了10海里后到
达点B,这时测得小岛O在北偏东45°,船继续航行到点C时,测得小岛O恰好在船的正北方,求
此时船到小岛的距离. (结果保留根号)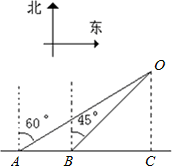
如图,四边形ABCD中,点E、F分别为AB、AD的中点,且EF=3,BC=10,CD=8,求cosC.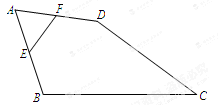
在一个箱子中放有三张完全相同的卡片,卡片上分别标有数字1,2,3.从箱子中任意取出一张卡片,用卡片上的数字作为十位数字,放回后搅匀,再取出一张卡片,用卡片上的数字作为个位数字,这样组成一个两位数.请用列表法或画树状图的方法完成下列问题:
(1)按这种方法能组成哪些两位数?
(2)组成的两位数是偶数的概率是多少?