如图，抛物线
与直线
交于C，D两点，其中点C在y轴上，点D的坐标为
。点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F.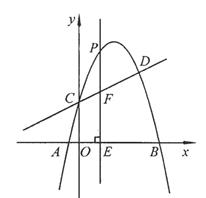
（1）求抛物线的解析式；
（2）若点P的横坐标为m，当m为何值时，以O，C，P，F为顶点的四边形是平行四边形？请说明理由；
（3）若存在点P，使∠PCF=450，请直接写出相应的点P的坐标。
如图，求∠A+∠B+∠C+∠D+∠E+∠F的值。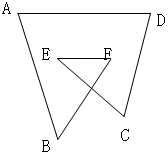
常州春秋旅行社为吸引市民组团去天水湾风景区旅游，推出了如下收费标准：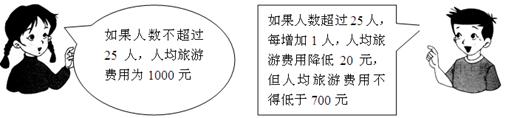
某单位组织员工去天水湾风景区旅游，共支付给春秋旅行社旅游费用27000元，请问该单位这次共有多少员工去天水湾风景区旅游？
某同学根据很久以前的某省内五个城市商品房销售均价（即销售平均价）的数据，绘制了如下统计图：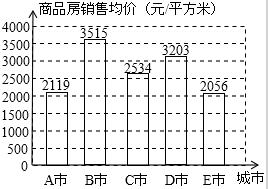
（1）这五个城市该年年商品房销售均价的中位数、极差分别是多少？
（2）若前两年年A城市的商品房销售均价为1600元/平方米，试估计A城市从前两年到
该年商品房销售均价的年平均增长率约是多少（要求误差小于1%）？
在解一元二次方程时，粗心的甲、乙两位同学分别抄错了同一道题，甲抄错了常数项，得到的两根分别是8和2；乙抄错了一次项系数，得到的两根分别是-9和-1.你能找出正确的原方程吗？若能，请你用配方法求出这个方程的根.
某工程队再我市实施棚户区改造过程中承包了一项拆迁工程。原计划每天拆迁1250m2，因为准备工作不足，第一天少拆迁了20％。从第二天开始，该工程队加快了拆迁速度，第三天拆迁了1440m2。
求：(1)该工程队第一天拆迁的面积；
(2)若该工程队第二天、第三天每天的拆迁面积比前一天增加的百分数相同，求这个百分数。