某班有50位学生，每位学生都有一个序号，将50张编有学生序号（从1号到50号）的卡片（除序号不同外其它均相同打乱顺序重新排列，从中任意抽取1张卡片
（1）在序号中，是20的倍数的有：20，40，能整除20的有：1，2，4，5，10（为了不重复计数，20只计一次），求取到的卡片上序号是20的倍数或能整除20的概率；
（2）若规定：取到的卡片上序号是k（k是满足1≤k≤50的整数），则序号是k的倍数或能整除k（不重复计数）的学生能参加某项活动，这一规定是否公平？请说明理由；
（3）请你设计一个规定，能公平地选出10位学生参加某项活动，并说明你的规定是符合要求的．
已知：如图，一次函数
的图象与反比例函数
（
）的图象交于点
．
轴于点
，
轴于点
．一次函数的图象分别交
轴、
轴于点
、点
， 
，且tan∠PDB=
．
求点
的坐标；求一次函数与反比例函数的解析式；
根据图象写出当
取何值时，一次函数的值小于反比例函数的值?
小明和小颖做掷骰子的游戏，规则如下：①游 戏前，每人选一个数字；②每次同时掷两枚均匀骰子；③如果同时掷得的两枚骰子点数之和，与谁所选数字相同，那么谁就获胜．用列表法或树状图列出同时掷两枚均匀骰子所有可能出现的结果：
小明选的数字是5，小颖选的数字是8．如果你也加入游戏，你会选什么数字，使自己获胜的概率比他们大？请说明理由．
根据第五次、第六次全国人口普查结果显示：某市常住人口总数由第五次的400万人增加到第六次的450万人，常住人口的学历状况统计图如下（部分信息未给出）：
解答下列问题：计算第六次人口普查小学学历的人数，并把条形统计图补充完整；
第六次人口普查结果与第五次相比，该市常住人口中高中学历人数增长的百分比是多少？
如图，△ABC和△ECD都是等腰直角三角形，∠ACB=∠DCE=900，D为AB边上一点，求证：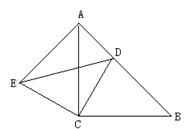
△ACE≌△BCD
已知AD=3，AB=7，求DE的长。
化简求值：
，其中
．