如图，抛物线y=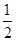
x2+mx+n交x轴于A、B两点，交y轴于点C，点P是它的顶点，点A的横坐标是-3，点B的横坐标是1．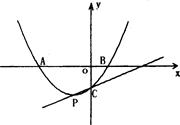
(1)求m、n的值；
(2)求直线PC的解析式；
(3)请探究以点A为圆心、直径为5的圆与直线PC的位置关系，并说明理由．(参考数据：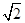
≈1.41，
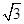≈1.73，
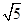≈2.24)
如图，AB⊥EF，DC⊥EF，垂足分别为B、C,且AB=CD,BE=CF．AF、DE相交于点O，AF、DC相交于点N,DE、AB相交于点M．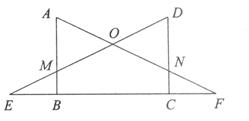
（1）请直接写出图中所有的等腰三角形；
（2）求征：△ABF≌△DCE．
1995年联合国教科文组织把每年4月23日确定为“世界读书日”．为了解某市市民每天阅读书籍的时间，某调查统计公司准备采用以下调查方式中的一种进行调查：①从该市一所大学里随机选取300名学生；
②分别从该市一所小学、一所中学、一所大学各随机选取100名学生，共选取300名学生；
③从该市三个不同的住宅小共中随机选取300名市民；
④从该市公安局户籍管理处随机抽取300名市民作为调查对象，然后进行调查．（1）在上述调查方式中，你认为比较合理的一个是（填序号）．
（2）由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图，在这个调查中，这300名市民每天阅读时间在2~3小时的人数是多少？
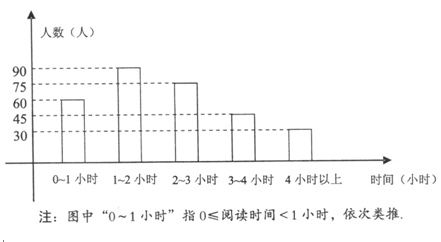
（3）若该市有360万人，请你利用（2）中的调查结果，估计该市每天阅读时间在2小时及以上的人数是多少？
（4）你认为这个调查活动中比较合理的高计中有没有可以进一步改进的地方？谈谈你的理由．
先化简，再求值．
（本题9分）如图9，已知二次函数
（
）的图象经过点
，
，
，直线
（
）与
轴交于点
．
（1）求二次函数的解析式；
（2）在直线
（）上有一点
（点在第四象限），使得
为顶点的三角形与以
为顶点的三角形相似，求点坐标（用含
的代数式表示）；（3）在（2）成立的条件下，抛物线上是否存在一点
，使得四边形
为平行四边形？若存在，请求出F点的坐标；若不存在，请说明理由．
（本题9分）如图，AB是半圆O的直径，E是的中点，OE交弦BC于点D，过
点C作⊙O切线交OE的延长线于点F. 已知BC=8，DE=2.
（1）求⊙O的半径；
（2）求CF的长；
（3）求tan∠BAD的值