某工厂计划为学校生产A,B两种型号的学生桌椅500套,以解决1254名学生的学习问题,一套A型桌椅(一桌两椅)需木料0.5m3,一套B型桌椅(一桌三椅)需木料0.7m3,工厂现有库存木料302m3。
(1)有多少种生产方案?
(2)现要把生产的全部桌椅运往学校销售,已知每套 型桌椅售价150元,生产成本100元,运费2元;每套
型桌椅售价150元,生产成本100元,运费2元;每套 型桌椅售价200元,生产成本120元,运费4元,求总利润
型桌椅售价200元,生产成本120元,运费4元,求总利润 (元)与生产
(元)与生产 型桌椅
型桌椅 (套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润
(套)之间的关系式,并确定总利润最少的方案和最少的总利润。(利润 售价-生产成本-运费)
售价-生产成本-运费)
(3)按(2)的方案计算,有没有剩余木料?如果有,请直接写出用剩余木料再生产以上两种型号的桌椅,最多还可以为多少名学生提供桌椅;如果没有,请说明理由。
如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.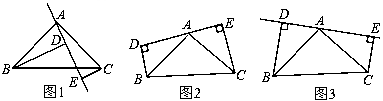
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=4,PE=1.
(1)求证:∠BPQ=60°(提示:利用三角形全等、外角的性质)
(2)求BE的长.
如图所示,已知点A,F,E,C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.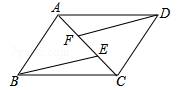
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.
△ABC在平面直角坐标系中的位置如图所示.A、B、C三点在格点上.作出△ABC关于y对称的△A1B1C1,并写出点△A1B1C1的坐标.
先化简,再求值: ,其中x=3
,其中x=3