如图甲，把一个边长为2的大正方形分成四个同样大小的小正方形，再连结大正方形的四边中点，得到了一个新的正方形（图中阴影部分），求:
（1）图甲中阴影部分的面积是多少？
（2）图甲中阴影部分正方形的边长是多少？
（3）如图乙，在数轴上以1个单位长度的线段为边作一个正方形，以表示数1的点为圆心，以正方形对角线长为半径画弧，交数轴负半轴于点A，求点A所表示的数是多少？
观察下列等式，你会发现什么规律：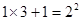
……
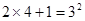
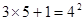
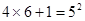
请将你发现的规律用仅含字母n（n为正整数）的等式表示出来，并说明它的正确性。
现有100元和20元的人民币共33张，总面额1620元.这两种人民币各多少元？
已知方程组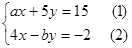
，由于甲看错了方程(1)中的a得到方程组的解为
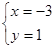，乙看错了方程（2）中的b得到方程组的解为
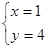．若按正确的a、b计算，求原方程组的解．
若x＋y=3，xy=1，试分别求出( x－y)2 和 x3 y＋ x y3的值（请写出具体的解题过程）
小亮和小明进行赛跑训练，他们选择了一个土坡，按同一路线同时出发，从坡脚跑到坡顶再原路返回坡脚．他们俩上坡的平均速度不同，下坡的平均速度则是各自上坡平均速度的1.5倍．设两人出发x min后距出发点的距离为y m．图中折线表示小亮在整个训练中y与x的函数关系，其中A点在x轴上，M点坐标为(2，0)．A点坐标为，A点所表示的实际意义是；
求出AB所在直线的函数关系式；
如果小明上坡平均速度是小亮上坡平均速度的一半，那么两人出发后多长时间
第一次相遇？