小亮和小明进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).A点坐标为 ,A点所表示的实际意义是 ;
求出AB所在直线的函数关系式;
如果小明上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间
第一次相遇?
一次函数 与反比例函数
与反比例函数 的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
的图象相交于A(﹣1,4),B(2,n)两点,直线AB交x轴于点D.
(1)求一次函数与反比例函数的表达式;
(2)过点B作BC⊥y轴,垂足为C,连接AC交x轴于点E,求△AED的面积S.
某服装店购进一批甲、乙两种款型时尚T恤衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的T恤衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批T恤衫商店共获利多少元?
如图,抛物线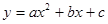 (
(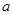 ≠0)与
≠0)与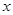 轴交于A(-4,0),B(2,0),与
轴交于A(-4,0),B(2,0),与 轴交与点C(0,2).
轴交与点C(0,2).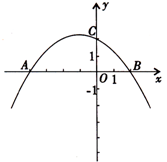
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;(解题用图见答题卡)
(3)以AB为直径作⊙M,直线经过点E(-1,-5),并且与⊙M相切,求该直线的解析式.(解题用图见答题卡)
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD—AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本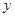 (万元/吨)与产量
(万元/吨)与产量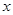 (吨)之间是一次函数关系,函数
(吨)之间是一次函数关系,函数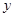 与自变量
与自变量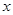 的部分对应值如下表:
的部分对应值如下表:
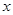 (吨) (吨) |
10 |
20 |
30 |
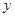 (万元/吨) (万元/吨) |
45 |
40 |
35 |
(1)求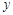 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量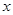 的取值范围;
的取值范围;
(2)当投入生产这种产品的总成本为1200万元时,求该产品的总产量;(注:总成本=每吨成本×总产量)
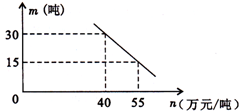
(3)市场调查发现,这种产品每月销售量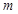 (吨)与销售单价
(吨)与销售单价 (万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)
(万元/吨)之间满足如图所示的函数关系.该厂第一个月按同一销售单价卖出这种产品25吨,请求出该厂第一个月销售这种产品获得的利润.(注:利润=售价—成本)