郑州市花卉种植专业户王有才承包了30亩花圃,分别种植康乃馨和玫瑰花,有关成本、销售额见下表:
| 种植种类 |
成本(万元/亩) |
销售额(万元/亩) |
| 康乃馨 |
2.4 |
3 |
| 玫瑰花 |
2 |
2.5 |
(1)2012年,王有才种植康乃馨20亩、玫瑰花10亩,求王有才这一年共收益多少万元?(收益=销售额-成本)
(2)2013年,王有才继续用这30亩花圃全部种植康乃馨和玫瑰花,计划投入成本不超过70万元.若每亩种植的成本、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花各多少亩?
(3)已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg,根据(2)中的种植亩数,为了节约运输成本,实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍,结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克?
如图,在平行四边形ABCD中,E为BC边上一点,连结AE、BD且AE=AB。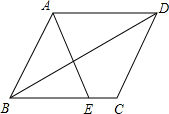
(1)求证:∠ABE=∠EAD;
(2)若∠AEB=2∠ADB,求证:四边形ABCD是菱形。
一只不透明的袋子中,装有分别标有数字1、2、3的三个球,这些除所外都相同,搅匀后从摸出个,记录下后放回袋并搅匀,再从任意摸出个,记录下,请用列表或画树状图方法,求出两次摸出上之和为偶数概率.
市交警支队对某校学生进行交通安全知识宣传,事先以无记名的方式随机调查了该部分闯红灯的情况,并绘制成如图所示的统计图.请根据图中的信息回答下列问题: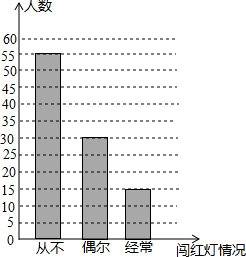
(1)本次共调查了多少名?
(2)如果该共有1500名,请你估计该经常闯红灯的大约有多少人;
(3)针图中反映的信息谈谈你的认识.(不超过30个字)。
先化简,再求值: ,其中x为方程
,其中x为方程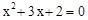 的根。
的根。
(1)计算::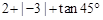 。
。
(2)解不等式: 。
。