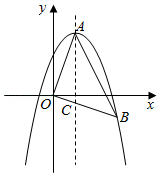
如图,在平面直角坐标系中,点 为坐标原点,抛物线 的顶点是 ,将 绕点 顺时针旋转 后得到 ,点 恰好在抛物线上, 与抛物线的对称轴交于点 .
(1)求抛物线的解析式;
(2) 是线段 上一动点,且不与点 , 重合,过点 作平行于 轴的直线,与 的边分别交于 , 两点,将 以直线 为对称轴翻折,得到△ ,设点 的纵坐标为 .
①当△ 在 内部时,求 的取值范围;
②是否存在点 ,使 ,若存在,求出满足条件 的值;若不存在,请说明理由.
.(本小题10分)
随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求:(1)该小区家庭轿车拥有量的年平均增长率是多少?
(2)该小区到2009年底家庭轿车将达到多少辆?
为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.
(本小题8分)
在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个. 现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
.(本题8分)
如图,AB是⊙O的直径,C是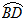 的中点,CE⊥AB于 E,BD交CE于点F.
的中点,CE⊥AB于 E,BD交CE于点F.
(1)求证:CF﹦BF;
(2)若CD ﹦6, AC ﹦8,则⊙O的半径为,CE的长是.
(本小题10分)
为迎接国庆60周年,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
请根据以上图表提供的信息,解答下列问题:(1)表中
 所表示的数分别为:
所表示的数分别为: ;
;(2)请在右图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
(本小题10分)
如图,在平面直角坐标系中, 的三个顶点的坐标分别为
的三个顶点的坐标分别为 .
.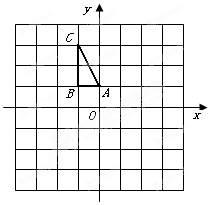
(1)画出
 关于x轴对称的
关于x轴对称的 ,并写出点
,并写出点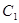 的坐标.
的坐标.(2)画出
 绕原点
绕原点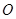 顺时针方向旋转90°后得到的
顺时针方向旋转90°后得到的 ,并写出点
,并写出点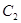 的坐标.
的坐标.(3)将
 平移得到
平移得到 ,使点
,使点 的对应点是
的对应点是 ,点
,点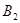 的对应点是
的对应点是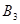 ,点
,点 的对应点是
的对应点是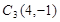 ,在坐标系中画出
,在坐标系中画出 ,并写出点
,并写出点 ,
,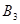 的坐标.
的坐标.