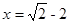一只不透明的袋子中,装有分别标有数字1、2、3的三个球,这些除所外都相同,搅匀后从摸出个,记录下后放回袋并搅匀,再从任意摸出个,记录下,请用列表或画树状图方法,求出两次摸出上之和为偶数概率.
如图,在一个边长为1的正方形网格上,把△ABC向右平移4个方格,再向上平移2个方格,得到△A′B′C′(A′ B′分别对应A、B).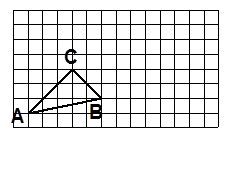
(1)请画出平移后的图形,并标明对应字母;(
2)求四边形AA′B′B的周长和面积.(结果保留根式)
某市自来水公司为限制单位用水,每月只给某单位计划内用水3000吨,计划内用水每吨收费0.5元,超计划部分每吨按0.8元收费.
(1)某月该单位用水3200吨,水费是※元;若用水2800吨,水费是※元;
(2)写出该单位水费y(元)与每月用水量x(吨)之间的函数关系式;
(3)若某月该单位缴纳水费1540元,则该单位这个月的用水多少吨?
已知反比例函数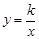 的图象经过(1,-2).
的图象经过(1,-2).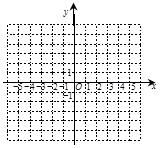
(1)求该反比例函数的解析式;
(2)选取适当的数据填入下表,并在如图所示的直角坐标系内描点画出该反比例函数的图象:
|
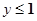 时,
时,
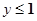 时,x的取值范围;当
时,x的取值范围;当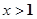 时,y的取值范围.
时,y的取值范围.
某专卖店开业首季度只试销A、B、C、D四种型号的电动自行车,试销结束后,经销人员绘制了如下两幅统计图,如图①和图②(均不完整).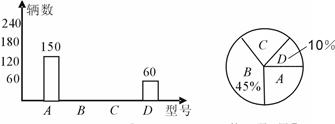
(1)该专卖店试销的四种型号中,型号的电动自行车的销售量最好;
(2)试销期间,该专卖店电动自行车总销量是多少?B型电动自行车、C型电动自行车的销售量分别是多少?
(3)如果要从首季度销售了的B、C型号的电动自行车中,随机抽取一台进行质量跟综,抽到型号B的概率是多少?
先化简,再求值: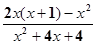 ,其中
,其中