如图是某地下商业街的入口,数学课外兴趣小组同学打算运用所学知识测量侧面支架最高点E到地面距离EF.经测量,支架立柱BC与地面垂直,即∠BCA=90°,且BC=1.5cm,点F、A、C在同一条水平线上,斜杆AB与水平线AC夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架边BE与AB夹角∠EBD=60°,又测得AD=1m。请你求出该支架边BE及顶端E到地面距离EF长度。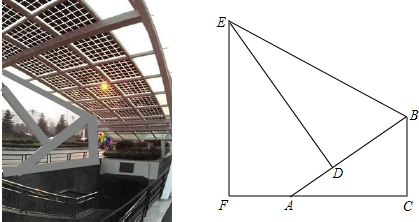
【改编题】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连接AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,tanB=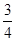 ,求⊙O的半径.
,求⊙O的半径.
【改编题】如图(1),在等边的顶点B、C处各有一只蜗牛,它们同时出发△ABC分别以每分钟1各单位的速度油B向C和由C向A爬行,其中一只蜗牛爬到终点s时,另一只也停止运动,经过t分钟后,它们分别爬行到D,P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?为什么?
(2)问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化?请证明你的结论.
(3)若蜗牛沿着BC和CA的延长线爬行,BD与AP交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中的∠DQA大小变化了吗?若无变化,请证明.若有变化,请直接写出∠DQA的度数.
【改编题】如图,在△ABC中,已知∠B=60°,∠C=30°,AE是△ABC角平分线,求: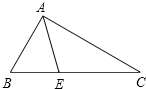
(1)作BC边上的高AD;
(2)∠DAE的度数.
如图,一次函数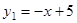 与反比例函数
与反比例函数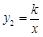 的图象交于A(1,m)、B(4,n)两点.
的图象交于A(1,m)、B(4,n)两点.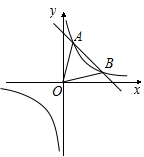
(1)求A、B两点的坐标和反比例函数的解析式;
(2)根据图象,直接写出当y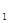 >y
>y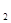 时x的取值范围;
时x的取值范围;
(3)求△AOB的面积.
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠。点O恰好落在弧AB上点D处,折痕交OA于点C,求整个阴影部分的周长和面积。