在平面直角坐标系xOy中，曲线y=x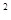
－6x+1与坐标轴的交点都在圆C上．
(Ⅰ)求圆C的方程；
(Ⅱ)试判断是否存在斜率为1的直线，使其与圆C交于A， B两点，且OA⊥OB，若存在，求出该直线方程，若不存在，请说明理由．
(本小题满分12分）
已知椭圆C的对称中心为原点O，焦点在x轴上，左右焦点分别为
和
，且||=2，
点（1，
）在该椭圆上.
（Ⅰ）求椭圆C的方程；
（Ⅱ）过的直线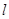
与椭圆C相交于A，B两点，若
AB的面积为
，求以为圆心且与直线
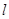相切是圆的方程.
(本小题满分12分）
我校高三年级进行了一次水平测试.用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计成绩的分组及各组的频数如下:
[40,50), 2; [50,60), 3; [60,70), 10; [70,80), 15; [80,90), 12; [90,100], 8.
（Ⅰ）完成样本的频率分布表；画出频率分布直方图.
（Ⅱ）估计成绩在85分以下的学生比例；
（Ⅲ）请你根据以上信息去估计样本的众数、中位数、平均数.（精确到0.01）
．(本小题满分12分）
如图，四棱锥P—ABCD中，底面ABCD是边长为
的正方形E，F分别为PC，BD的中点，侧面PAD⊥底面ABCD，且PA=P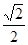D=
AD.
（Ⅰ）求证：EF//平面PAD；
（Ⅱ）求三棱锥C—PBD的体积.
(本小题满分12分）
已知公比大于1的等比数列{
}满足：
+
+
=28，且+2是和的等差中项.
（Ⅰ）求数列{}的通项公式；
（Ⅱ）若
=
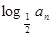，求{}的前n项和
.
（本小题满分12分）
已知函数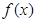
的定义域为
，且同时满足下列条件：
（1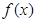）是奇函数；
（2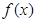）在定义域上单调递减；
（3）
求
的取值范围