(1)如图,ΔABC中,∠ABC=50°,∠ACB=70°,D为边BC上一点(D与B、C不重合),连接AD,∠ADB的平分线所在直线分别交直线AB、AC于点E、F. 求证:2∠AED-∠CAD=170°;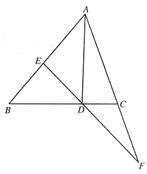
(2)若∠ABC=∠ACB=n°,且D为射线CB上一点,(1)中其他条件不变,请直接写出∠AED与∠CAD的数量关系.(用含n的代数式表示)
如图1,等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合,将此三角板绕点A旋转,使三角板中该锐角的两条边分别交正方形的两边BC,DC于点E,F,连接EF.
(1)猜想BE、EF、DF三条线段之间的数量关系,并证明你的猜想;
(2)在图1中,过点A作AM⊥EF于点M,请直接写出AM和AB的数量关系;
(3)如图2,将Rt△ABC沿斜边AC翻折得到Rt△ADC,E,F分别是BC,CD边上的点,∠EAF=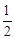 ∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.
∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想AM与AB之间的数量关系.并证明你的猜想.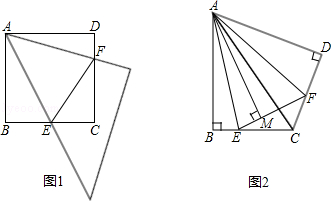
甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?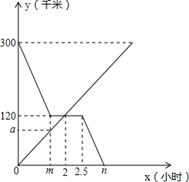
如图,AB是⊙O的直径,C是⊙O上一点,OD⊥BC于点D,过点C作⊙O的切线,交OD的延长线于点E,连接BE.
(1)求证:BE与⊙O相切;
(2)设OE交⊙O于点F,若DF=1,BC=2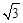 ,求由劣弧BC、线段CE和BE所围成的图形面积S.
,求由劣弧BC、线段CE和BE所围成的图形面积S.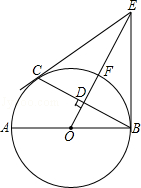
如图,某公司入口处有一斜坡AB,坡角为12°,AB的长为3m,施工队准备将斜坡修成三级台阶,台阶高度均为hcm,深度均为30cm,设台阶的起点为C.
(1)求AC的长度;
(2)求每级台阶的高度h.
(参考数据:sin12°≈0.2079,cos12°≈0.9781,tan12°≈0.2126.结果都精确到0.1cm)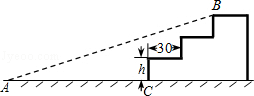
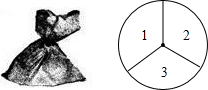
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.