如图1,△ABC中,CA=CB,点O在高CH上,OD⊥CA于点D,OE⊥CB于点E,以O为圆心,OD为半径作⊙O.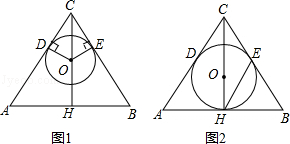
(1)求证:⊙O与CB相切于点E;
(2)如图2,若⊙O过点H,且AC=5,AB=6,连接EH,求△BHE的面积和tan∠BHE的值.
已知:正方形ABCD,GF∥BE,求证:EF·AE=BE·EC.
列方程解实际问题:2009年4月7日,国务院公布了《医药卫生体制改革近期重点实施方案(2009~2011年》,某市政府决定2009年用于改善医疗卫生服务的经费为6000万元,并计划2011年提高到7260万元,若从2009年到2011年每年的资金投入按相同的增长率递增,求2009年到2011年的年平均增长率.
如图,在△ACD中,B为AC上一点,且 ,
, ,
,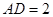 ,求AB的长.
,求AB的长.
关于x的一元二次方程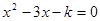 有两个不相等的实数根.
有两个不相等的实数根.
(1)求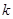 的取值范围;
的取值范围;
(2)若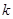 为符合条件的最小整数,求此时方程的根.
为符合条件的最小整数,求此时方程的根.
已知:二次函数的图象经过原点,对称轴是直线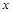 =-2,最高点的纵坐标为4,
=-2,最高点的纵坐标为4,
求:该二次函数解析式。