某面包厂2011年利润为100万元,因市场竞争,若不开发新项目,预测从2012年起每年利润比上一年减少4万元.2012年初,该面包厂一次性投入90万元开发新项目,预测在未扣除开发所投入资金的情况下,第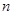 年(
年(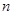 为正整数,2012年为第一年)的利润为
为正整数,2012年为第一年)的利润为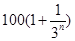 万元.设从2012年起的前
万元.设从2012年起的前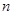 年,该厂不开发新项目的累计利润为
年,该厂不开发新项目的累计利润为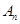 万元,开发新项目的累计利润为
万元,开发新项目的累计利润为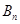 万元(须扣除开发所投入资金).
万元(须扣除开发所投入资金).
(1)求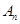 ,
,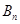 的表达式;
的表达式;
(2)问该新项目的开发是否有效(即开发新项目的累计利润超过不开发新项目的累计利润),如果有效,从第几年开始有效;如果无效,请说明理由.
已知数列 满足:
满足: ,且存在大于1的整数k使
,且存在大于1的整数k使 。
。
(1)用 表示m(不必化简)
表示m(不必化简)
(2)用k表示m(化成最简形式)
(3)若m是正整数,求k与m的值;
已知:经过点 的动圆与y轴交于M、N两点,C(-1,0),D(1,0)是x轴上两点,直线MC与
的动圆与y轴交于M、N两点,C(-1,0),D(1,0)是x轴上两点,直线MC与 ND相交于P。
ND相交于P。
(1)求点P的轨迹E的方程;
(2)直线GH交轨迹E于G、H两点,并且 (O是坐标原点),求点O到直线GH的距离。
(O是坐标原点),求点O到直线GH的距离。
已知a为实数,函数
(I)若函数 的图象上有与x轴平行的切线,求a的取值范围;
的图象上有与x轴平行的切线,求a的取值范围;
(II)当 时,对任意
时,对任意 恒成立,试求m的取值范围。
恒成立,试求m的取值范围。
袋中有大小相同的5个球,其中黑球3个,白球2个,甲乙二人分别从中各取一个,甲先取(不放回)乙后取。规定: 两人取到同颜色的球,由甲胜,取到不同颜色的球,则乙胜。
两人取到同颜色的球,由甲胜,取到不同颜色的球,则乙胜。
(1)分别求甲乙取到黑球的概率;
(2)甲乙二人谁胜的概率大,请说明理由。
如图在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,过D与PB垂直的平面分别交PB、PC于F、E。PD=DC。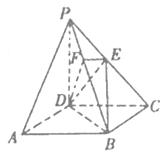
(1)求证:DE⊥PC
(2)求证:PA//平面EDB;
(3)求二面角C—PB—D的大小。