已知定义在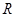 上的函数
上的函数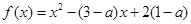 (其中
(其中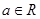 ).
).
(Ⅰ)解关于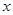 的不等式
的不等式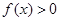 ;
;
(Ⅱ)若不等式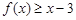 对任意
对任意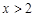 恒成立,求
恒成立,求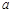 的取值范围.
的取值范围.
(本小题满分14分)
已知数列{an}中,a1="1" ,a2=3,且点(n,an)满足函数y = kx + b.
(1)求k,b的值,并写出数列{an}的通项公式;
(2)记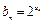 ,求数列{bn}的前n和Sn.
,求数列{bn}的前n和Sn.
(本小题满分12分)
设函数 ,其中向量
,其中向量 ,
, ,
, ,且
,且 的图象经过点
的图象经过点 .(1)求实数
.(1)求实数 的值;
的值;
(2)求函数 的最小值及此时
的最小值及此时 值的集合.
值的集合.
(本小题满分12分)
不等式mx2-mx+1>0,对任意实数x都成立,求m的取值范围。
(本小题满分14分)
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n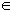 N+,都有
N+,都有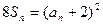 。
。
(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设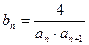 ,
,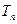 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得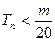 对所有n
对所有n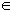 N+都成立的最小正整数
N+都成立的最小正整数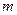 的值。
的值。
(本小题满分14分)
一农民有基本农田2亩,根据往年经验,若种水稻,则每季每亩产量为400公斤;若种花生,则每季每亩产量为100公斤。但水稻成本较高,每季每亩240元,而花生只需80元,且花生每公斤5元,稻米每公斤卖3元。现该农民手头有400元,两种作物各种多少,才能获得最大收益?