(本小题满分14分)如图,在底面是矩形的四棱锥 中,
中, 平面
平面 ,
, ,
, 是
是 的中点.
的中点.
(1)求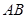 与平面
与平面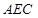 所成的角的正弦值;
所成的角的正弦值;
(2)若点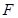 在线段
在线段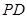 上,二面角
上,二面角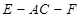 所成角为
所成角为 ,
,
且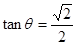 ,求
,求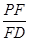 的值.
的值.
、选修4-5:不等式选讲
设函数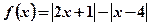 。(1)求不等式
。(1)求不等式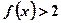 的解集;(2)求函数
的解集;(2)求函数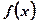 的最小值
的最小值
选修4-4:极坐标与参数方程
已知直线的极坐标方程为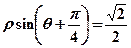 ,圆
,圆 的参数方程为
的参数方程为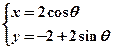 (其中
(其中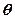 为参数)
为参数)
(1)将直线的极坐标方程化为直角坐标方程;(2)求圆 上的点到直线的距离的最小值
上的点到直线的距离的最小值
选修4-1:几何证明选讲
如图 内
内 接于圆
接于圆 ,
,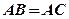 ,直线
,直线 切圆
切圆 于点
于点 ,弦
,弦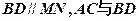 相交于点
相交于点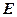 。(1)求证
。(1)求证 ≌
≌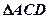 ;(2)若
;(2)若
(本小题满分1 2分)
2分)
已知函数 ,函数
,函数 是区间[-1,1]上的减
是区间[-1,1]上的减 函数.
函数.
(I)求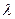 的最大值;
的最大值;
(II)若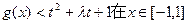 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程 的根的个数.
的根的个数.
(本小题满分1 2分)
2分)
设 、
、 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
(Ⅰ)若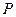 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求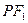 ·
· 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点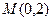 的直线
的直线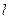 与椭圆交于不同的两点
与椭圆交于不同的两点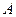 、
、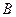 ,且∠
,且∠ 为锐角(其中
为锐角(其中 为坐标原点),求直线
为坐标原点),求直线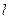 的斜率
的斜率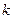 的取值范围.
的取值范围.