某公共汽车的运行非常规则,先由静止开始匀加速启动,当速度达到v1=10 m/s时再做匀速运动,进站前开始匀减速制动,在到达车站时刚好停住.公共汽车在每个车站停车时间均为Δt=25 s,然后以同样的方式运行至下一站.已知公共汽车在加速启动和减速制动时加速度大小都为a=1 m/s2,而所有相邻车站间的行程都为x=600 m.有一次当公共汽车刚刚抵达一个车站时,一辆电动车刚经过该车站一段时间t0=60 s,已知该电动车速度大小恒定为v2=6 m/s,而且行进路线、方向与公共汽车完全相同,不考虑其他交通状况的影响,试求:
(1)公共汽车从其中一车站出发至到达下一站所需的时间t;
(2)若从下一站开始计数,公共汽车在刚到达第n站时,电动车也恰好同时到达此车站,n为多少?
如图所示,固定的半圆形绝缘光滑轨道置于正交的匀强电场和匀强磁场叠加的区域中。轨道半径为R,磁感应强度为B,方向垂直于纸面向外,电场强度为E,方向水平向左。
(1)一个质量为m的小球(可视为质点)放在轨道上的C点恰好处于静止,圆弧半径OC与水平直径AD的夹角为α(sinα=0.8,cosα=0.6)。求小球所电荷量;试说明小球带何种电荷并陈述理由。
(2)如果将小球从A点由静止释放,小球在圆弧轨道上运动时,对轨道的最大压力是多少?
(3) 若将小球从A点由静止释放,小球沿圆弧轨道运动到最低点时,与另一个质量也为m且静止在O点正下方P点的不带电小球(可视为质点)发生碰撞,设碰撞过程历时可以忽略且无机械能损失也无电荷转移。两小球在运动过程中始终没有脱离圆弧轨道。求第一次碰撞后到第二次碰撞前,两小球在圆弧轨道上上升的最大高度各是多少?
如图所示,在竖直面内有一个光滑弧形轨道,其末端水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接。A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧。两滑块从弧形轨道上的某一高度由静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动通过轨道最高点时对轨道的压力大小恰等于其所受重力的大小。已知圆形轨道的半径R=0.60m,滑块A的质量mA=0.16kg,滑块B的质量mB=0.04kg,两滑块开始下滑时距圆形轨道底端的高度h=0.80m,重力加速度g取10m/s2,空气阻力可忽略不计。求:
(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小;
(2)滑块A被弹簧弹开时的速度大小;
(3)弹簧在将两滑块弹开的过程中释放的弹性势能。
如图所示,倾角的斜面底端B平滑连接着半径r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块,从距地面h=2.7m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数=0.25,求:(sin37=0.6,cos37=0.8,g=10m/s2)
(1)(5)物块滑到斜面底端B时的速度大小。
(2)(7)物块沿圆轨道运动到最高点A后在空中做平抛运动落在OB水平面上,已知平抛运动水平位移为1.8m,求物块运动至A点时对圆轨道的压力大小。
如图所示,跳台滑雪运动员经过一段加速滑行后从O点水平飞出,经3.0s落到斜坡上的A点。已知O点是斜坡的起点,斜坡与水平面的夹角=37,运动员的质量m=50kg。不计空气阻力。(取sin37=0.60,cos37=0.80;g取10m/s2)求
(1)(5)A点与O点的距离L;
(2)(5)运动员离开O点时的速度大小。
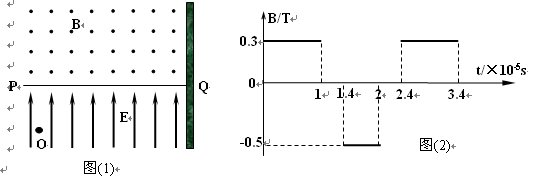
如图1所示,水平直线PQ下方有竖直向上的匀强电场,上方有垂直纸面方向的磁场,其磁感应强度B随时间的变化规律如图2所示(磁场的变化周期T=2.4×10-5s)。现有质量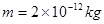 带电量为
带电量为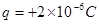 的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0=
的点电荷,在电场中的O点由静止释放,不计电荷的重力。粒子经t0=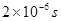 第一次以
第一次以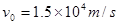 的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取
的速度通过PQ,并进入上方的磁场中。取磁场垂直向外方向为正,并以粒子第一次通过PQ时为t=0时刻。(本题中取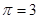 ,重力加速度
,重力加速度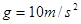 )。试求:
)。试求:
⑴ 电场强度E的大小;
⑵  时刻电荷与O点的水平距离;
时刻电荷与O点的水平距离;
⑶ 如果在O点右方d=67.5cm处有一垂直于PQ的足够大的挡板,求电荷从开始运动到碰到挡板所需的时间。(保留三位有效数字)