如右图，在
区域内存在与xy平面垂直的匀强磁场，磁感应强度的大小为B.在t＝0时刻，一位于坐标原点的粒子源在xy平面内发射出大量同种带电粒子，所有粒子的初速度大小相同，方向与y轴正方向的夹角分布在0～180°范围内．已知沿y轴正方向发射的粒子在
时刻刚好从磁场边界上
点离开磁场．求：
(1)粒子在磁场中做圆周运动的半径R及粒子的比荷q/m；
(2)此时刻仍在磁场中的粒子的初速度方向与y轴正方向夹角的取值范围；
(3)从粒子发射到全部粒子离开磁场所用的时间。
两个完全相同的电热器，分别通过如图a和b所示的电流最大值相等的方波交变电流和正弦交变电流，则这两个电热器的电功率之比Pa∶Pb等于多少？
(16分)一个电阻为r、边长为L的正方形线圈abcd共N匝,线圈在磁感应强度为B的匀强磁场中绕垂直于磁感线的轴OO′以如图所示的角速度ω匀速转动,外电路电阻为R.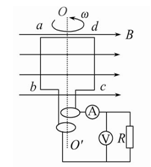
(1)在图中标出此刻线圈感应电流的方向.
(2)线圈转动过程中感应电动势的最大值有多大?
(3)线圈平面与磁感线夹角为60°时的感应电动势为多大?
(4)设发电机由柴油机带动,其他能量损失不计,线圈转一周,柴油机做多少功?
(5)从图示位置开始,线圈转过60°的过程中通过R的电量是多少?
(6)图中电流表和电压表的示数各是多少?
电阻可忽略的光滑平行金属导轨长S=1.15m，两导轨间距L="0.75" m，导轨倾角为30°，导轨上端ab接一阻值R=1.5Ω的电阻，磁感应强度B=0.8T的匀强磁场垂直轨道平面向上。阻值r=0.5Ω，质量m=0.2kg的金属棒与轨道垂直且接触良好，从轨道上端ab处由静止开始下滑至底端，在此过程中金属棒产生的焦耳热
。(取
)求：
(1)金属棒在此过程中克服安培力的功
；
(2)金属棒下滑速度
时的加速度
．
(3)为求金属棒下滑的最大速度
，有同学解答如下：由动能定理
，……。由此所得结果是否正确？若正确，说明理由并完成本小题；若不正确，给出正确的解答。
有人设计了一种可测速的跑步机，测速原理如题23图所示，该机底面固定有间距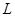为
、长度为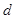
的平行金属电极。电极间充满磁感应强度为
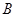、方向垂直纸面向里的匀强磁场，且接有电压表和电阻
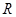,绝缘橡胶带上镀有间距为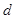的平行细金属条，磁场中始终仅有一根金属条，且与电极接触良好，不计金属电阻，若橡胶带匀速运动时，电压表读数为
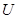,求：
⑴橡胶带匀速运动的速率；
⑵电阻R消耗的电功率；
⑶一根金属条每次经过磁场区域克服安培力做的功。
如图，两根足够长的金属导轨ab、cd竖直放置，导轨间距离为L电阻不计。在导轨上端并接两个额定功率均为P、电阻均为R的小灯泡。整个系统置于匀强磁场中，磁感应强度方向与导轨所在平面垂直。现将一质量为m、电阻可以忽略的金属棒MN从图示位置由静止开始释放。金属棒下落过程中保持水平，且与导轨接触良好。已知某时刻后两灯泡保持正常发光。重力加速度为g。求：
(1)磁感应强度的大小：
(2)灯泡正常发光时导体棒的运动速率。