已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在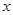 轴上,离心率
轴上,离心率 ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线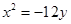 的焦点.
的焦点.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 与曲线
与曲线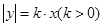 的交点为
的交点为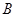 、
、 ,求
,求 面积的最大值.
面积的最大值.
(1)求函数 的表达式,并求其定义域。
的表达式,并求其定义域。
(2)当 时,求函数
时,求函数 的值域
的值域
(1)求博物馆支付总费用y与保护罩容积V之间的函数关系式;
(2)求博物馆支付总费用的最小值。

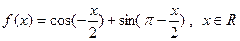

(1)求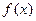 的周期;
的周期; (2)求
(2)求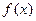 在
在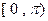 上的减区间;
上的减区间;
(3)若
 ,
,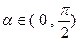 ,求
,求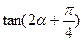 的值
的值
于定义在D上的函数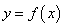 ,若同时满足
,若同时满足
①存在闭区间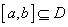 ,使得任取
,使得任取 ,都有
,都有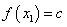 (
( 是常数);
是常数);
②对于D内任意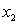 ,当
,当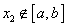 时总有
时总有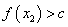 ;
;
则称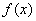 为“平底型”函数.
为“平底型”函数.
(1)判断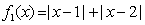 ,
,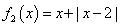 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设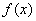 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若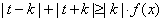 ,(
,(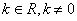 )
)
对一切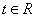 恒成立,求实数
恒成立,求实数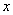 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和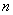 的值.
的值.
如图△ABC为正三角形,边长为2,以点A为圆心,1为半径作圆.
(1)若 ,求
,求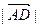 ;
;
(2)PQ为圆A的任意一条直径,求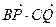 的最大值.
的最大值.