已知△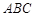 的两个顶点
的两个顶点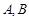 的坐标分别是
的坐标分别是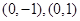 ,且
,且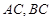 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点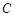 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当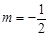 时,过点
时,过点 的直线
的直线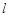 交曲线
交曲线 于
于 两点,设点
两点,设点 关于
关于 轴的对称
轴的对称
点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与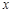 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
设函数
(1)设 的内角,且为钝角,求
的内角,且为钝角,求 的最小值;
的最小值;
(2)设 是锐角
是锐角 的内角,且
的内角,且 求
求 的三个内角的大小和AC边的长。
的三个内角的大小和AC边的长。
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
(1)求证:平面 平面
平面 ;
;
(2)在底面A1D1上有一个靠近D1的四等分点H,求证: EH∥平面FGB1;
(3)求四面体EFGB1的体积.
已知双曲线C的中心在原点,抛物线 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.
(1)求双曲线C的方程;
(2)若 ,求实数k值.
,求实数k值.
如图,四面体ABCD中,O、E分别是BD、BC的中点,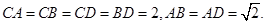
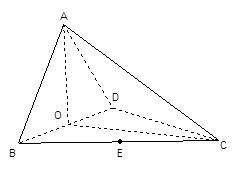
(I)求证: 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的余弦值;
(III)求点E到平面ACD的距离。
设函数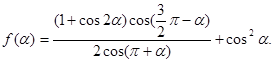
(1)设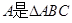 的内角,且为钝角,求
的内角,且为钝角,求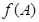 的最小值;
的最小值;
(2)设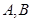 是锐角
是锐角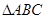 的内角,且
的内角,且 求
求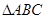 的三个内角的大小和AC边的长。
的三个内角的大小和AC边的长。