某市准备从7名报名者（其中男5人，女3人）中选3人参加三个副局长职务竞选.
（1）设所选3人中女副局长人数为
，求的分布列及数学期望.
（2）若选派三个副局长依次到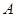
、
、
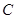三个局商上任，求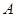局是男局长的情况下，局是女副局长的概率.
设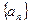
是公比为正数的等比数列，
，
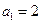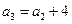
（Ⅰ）求
的通项公式；
（Ⅱ）设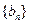
是首项为1，公差为2的等差数列，求数列
的前
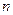项和
已知二次函数
（1）若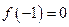
，试判断函数
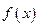零点个数
(2) 若对
且
，
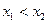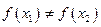，证明方程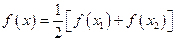
必有一个实数根属于
(3)是否存在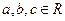
，使
同时满足以下条件①当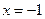
时， 函数有最小值0；；②对
,都有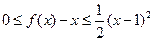
。若存在，求出
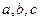的值，若不存在，请说明理由。
如图，正四棱锥S-ABCD的底面是边长为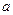
正方形，
为底面
对角线交点，侧棱长是底面边长的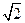
倍，P为侧棱SD上的点.
（Ⅰ）求证：AC⊥SD
（Ⅱ）若SD⊥平面PAC，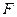
为
中点,求证:
∥平面PAC;
（Ⅲ）在（Ⅱ）的条件下，侧棱SC上是否存在一点E， 使得BE∥平面PAC.若存在，求SE：EC的值；若不存在，试说明理由。
某公司通过报纸和电视两种方式做销售某种商品的广告，根据统计资料，销售收入R(万元)与报纸广告费用x1(万元)及电视广告费用x2(万元)之间的关系有如下经验公式：R＝－2x12－x22＋13x1＋11x2－28.
(1)若提供的广告费用共为5万元，求最优广告策略．(即收益最大的策略，其中收益＝销售收入－广告费用)
(2)在广告费用不限的情况下，求最优广告策略
（本小题满分12分）
已知函数
，函数
（
，且
）
（Ⅰ）求函数
的定义域
（Ⅱ）求使函数的值为正数的
的取值范围