如图,直三棱柱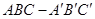 的侧棱长为3,
的侧棱长为3,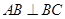 ,且
,且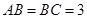 ,
, 、
、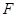 分别是棱
分别是棱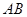 、
、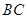 上的动点,且
上的动点,且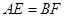
(1)证明:无论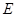 在何处,总有
在何处,总有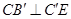 ;
;
(2)当三棱柱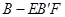 .的体积取得最大值时,求异面直线
.的体积取得最大值时,求异面直线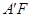 与
与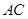 所成角的余弦值.
所成角的余弦值.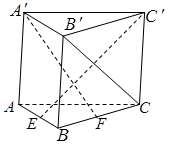
选修4—5:不等式选讲
已知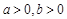 ,证明:
,证明: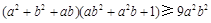 .
.
选修4—4:坐标系与参数方程
已知两个动点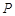 ,
,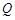 分别在两条直线
分别在两条直线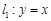 和
和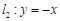 上运动,且它们的横坐标分别为角
上运动,且它们的横坐标分别为角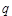 的正弦,余弦,
的正弦,余弦,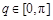 .记
.记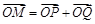 ,求动点
,求动点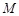 的轨迹的普通方程.
的轨迹的普通方程.
选修4—2:矩阵与变换
已知矩阵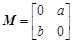 满足:
满足: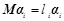 ,其中
,其中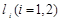 是互不相等的实常数,
是互不相等的实常数,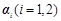 ,是非零的平面列向量,
,是非零的平面列向量,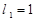 ,
,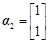 ,求矩阵
,求矩阵 .
.
选修4—1:几何证明选讲
已知AB是圆O的直径,P是上半圆上的任意一点,PC是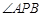 的平分线,
的平分线, 是下半圆的中点.求证:直线PC经过点
是下半圆的中点.求证:直线PC经过点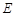 .
.
(本小题满分16分)已知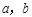 为实数,函数
为实数,函数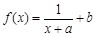 ,函数
,函数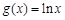 .
.
(1)当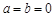 时,令
时,令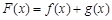 ,求函数
,求函数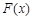 的极值;
的极值;
(2)当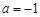 时,令
时,令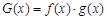 ,是否存在实数
,是否存在实数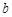 ,使得对于函数
,使得对于函数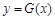 定义域中的任意实数
定义域中的任意实数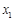 ,均存在实数
,均存在实数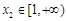 ,有
,有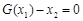 成立,若存在,求出实数
成立,若存在,求出实数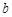 的取值集合;若不存在,请说明理由.
的取值集合;若不存在,请说明理由.