数列 满足
满足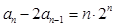
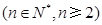 ,且
,且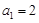 .
.
(1) 求数列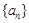 的通项公式;
的通项公式;
(2) 令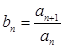 ,当数列
,当数列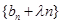 为递增数列时,求正实数
为递增数列时,求正实数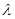 的取值范围.
的取值范围.
如图3所示,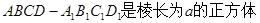 ,M是棱
,M是棱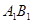 的中点,N是棱
的中点,N是棱 的中点.
的中点.
(1)求异面直线 所成角的正弦值;
所成角的正弦值;
(2)求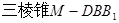 的体积.
的体积.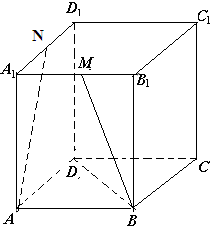
为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组、有关数据见下表(单位:人)
(1)求x,y ;
(2)若从高校B、C抽取的人中选2人作专题发言,求这二人都来自高校C的概率。
在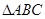 中,角
中,角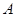 、
、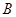 、
、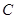 所对的边分别为
所对的边分别为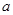 、
、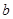 、
、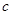 .若
.若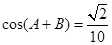 ,
, .(1)求
.(1)求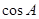 和
和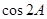 的值;(2)若
的值;(2)若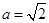 ,求
,求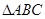 的面积.
的面积.
已知以点C (t, 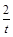 )(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
)(t∈R),t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为坐标原点.
(1)求证:△OAB的面积为定值;
(2)设直线y= –2x+4与圆C交于点M,N若|OM|=|ON|,求圆C的方程.
(3)若t>0,当圆C的半径最小时,圆C上至少有三个不同的点到直线l:y –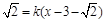 的距离为
的距离为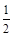 ,求直线l的斜率k的取值范围.
,求直线l的斜率k的取值范围.
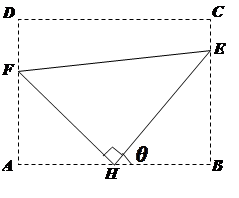
如图:某污水处理厂要在一个矩形污水处理池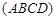 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道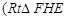 ,
, 是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口
是直角顶点)来处理污水,管道越长,污水净化效果越好.设计要求管道的接口 是
是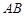 的中点,
的中点, 分别落在线段
分别落在线段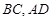 上.已知
上.已知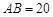 米,
米,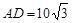 米,记
米,记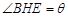 .
.
(1)试将污水净化管道的长度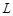 表示为
表示为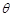 的函数,并写出定
的函数,并写出定
义域;
(2)若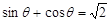 ,求此时管道的长度
,求此时管道的长度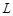 ;
;
(3)问:当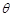 取何值时,污水净化效果最好?并求出此时
取何值时,污水净化效果最好?并求出此时
管道的长度.