给定椭圆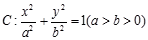 ,称圆心在坐标原点
,称圆心在坐标原点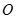 ,半径为
,半径为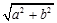 的圆是椭圆
的圆是椭圆 的“伴随圆”.若椭圆C的一个焦点为
的“伴随圆”.若椭圆C的一个焦点为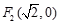 ,其短轴上的一个端点到
,其短轴上的一个端点到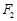 距离为
距离为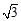 .
.
(Ⅰ)求椭圆 及其“伴随圆”的方程;
及其“伴随圆”的方程;
(Ⅱ)若过点 的直线与椭圆C只有一个公共点,且截椭圆C的“伴随圆”所得的弦长为
的直线与椭圆C只有一个公共点,且截椭圆C的“伴随圆”所得的弦长为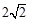 ,求
,求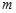 的值;
的值;
(Ⅲ)过椭圆C“伴随圆”上一动点Q作直线 ,使得
,使得 与椭圆C都只有一个公共点,试判断直线
与椭圆C都只有一个公共点,试判断直线 的斜率之积是否为定值,并说明理由.
的斜率之积是否为定值,并说明理由.
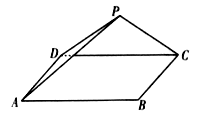
【2015高考广东,文18】(本小题满分14分)如图,三角形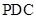 所在的平面与长方形
所在的平面与长方形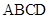 所在的平面垂直,
所在的平面垂直,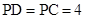 ,
,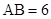 ,
,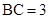 .
.
(1)证明: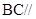 平面
平面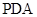 ;
;
(2)证明: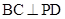 ;
;
(3)求点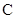 到平面
到平面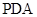 的距离.
的距离.
【2015高考福建,文20】如图, 是圆
是圆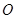 的直径,点
的直径,点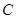 是圆
是圆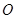 上异于
上异于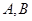 的点,
的点, 垂直于圆
垂直于圆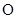 所在的平面,且
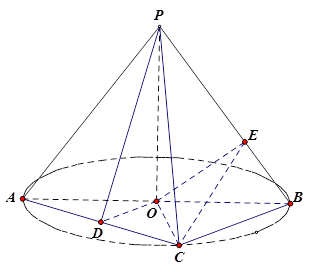
所在的平面,且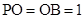 .
.
(Ⅰ)若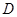 为线段
为线段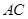 的中点,求证
的中点,求证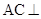 平面
平面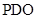 ;
;
(Ⅱ)求三棱锥 体积的最大值;
体积的最大值;
(Ⅲ)若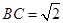 ,点
,点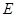 在线段
在线段 上,求
上,求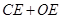 的最小值.
的最小值.
【2015高考北京,文18】(本小题满分14分)如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 且
且 ,
, ,
, 分别为
分别为 ,
,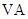 的中点.
的中点.
(Ⅰ)求证: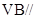 平面
平面 ;
;
(Ⅱ)求证:平面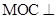 平面
平面 ;
;
(Ⅲ)求三棱锥 的体积.
的体积.
【2015高考安徽,文19】如图,三棱锥P-ABC中,PA 平面ABC,
平面ABC, .
.
(Ⅰ)求三棱锥P-ABC的体积;
(Ⅱ)证明:在线段PC上存在点M,使得AC BM,并求
BM,并求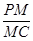 的值.
的值.
【2015高考上海,文22】本题共3个小题,第1小题4分,第2小题6分,第3小题6分.
已知椭圆 ,过原点的两条直线
,过原点的两条直线 和
和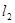 分别于椭圆交于
分别于椭圆交于 、
、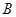 和
和 、
、 ,设
,设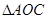 的面积为
的面积为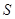 .
.
(1)设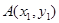 ,
,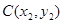 ,用
,用 、
、 的坐标表示点
的坐标表示点 到直线
到直线 的距离,并证明
的距离,并证明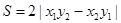 ;
;
(2)设 ,
,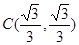 ,
,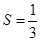 ,求
,求 的值;
的值;
(3)设 与
与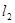 的斜率之积为
的斜率之积为 ,求
,求 的值,使得无论
的值,使得无论 与
与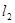 如何变动,面积
如何变动,面积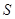 保持不变.
保持不变.