为调查乘客的候车情况,公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间(单位:分钟)作为样本分成5组,如下表所示:
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查,求抽到的两人恰好来自不同组的概率.
| 组别 |
候车时间 |
人数 |
| 一 |
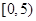 |
2 |
| 二 |
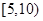 |
6 |
| 三 |
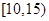 |
4 |
| 四 |
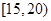 |
2 |
| 五 |
 |
1 |
已知向量 向量
向量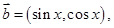 记
记
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若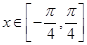 ,求函数
,求函数 的值域.
的值域.
已知椭圆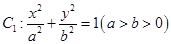 的离心率为
的离心率为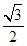 ,且经过点
,且经过点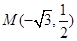 ,圆
,圆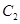 的直径为
的直径为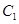 的长轴.如图,
的长轴.如图,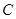 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线 过点
过点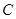 且与圆
且与圆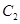 交于
交于 两点,
两点, 垂直于
垂直于 交椭圆于点
交椭圆于点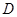 .
.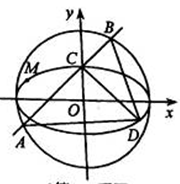
(1)求椭圆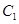 的方程;
的方程;
(2)求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.
已知函数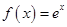 .
.
(1)设函数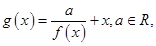 求
求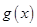 的极值.
的极值.
(2)证明: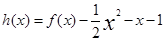 在
在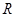 上为增函数。
上为增函数。
如图,在四棱锥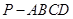 中,底面
中,底面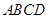 是边长为2的正方形,侧面
是边长为2的正方形,侧面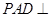 底面
底面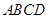 ,且
,且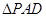 为等腰直角三角形,
为等腰直角三角形,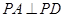 ,
,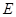 、
、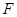 分别为
分别为 、
、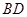 的中点.
的中点.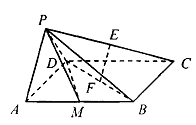
(1)求证: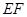 //平面
//平面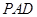 ;
;
(2)若线段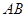 中点为
中点为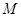 ,求二面角
,求二面角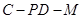 的余弦值.
的余弦值.
已知抛物线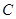 的顶在坐标原点,焦点
的顶在坐标原点,焦点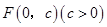 到直线
到直线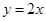 的距离是
的距离是
(1)求抛物线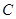 的方程;
的方程;
(2)若直线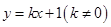 与抛物线
与抛物线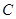 交于
交于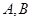 两点,设线段
两点,设线段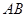 的中垂线与
的中垂线与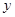 轴交于点
轴交于点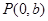 ,求
,求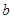 的取值范围.
的取值范围.