((本小题满分14分)设集合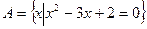 ,
,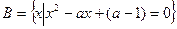 ,
,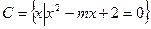 ,若
,若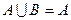 ,
,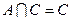 ,
,
(1)求实数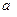 的取值集合.
的取值集合.
(2)求实数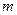 的取值集合.
的取值集合.
一架飞机从A地飞到B到,两地相距700km.飞行员为了避开某一区域的雷雨云层,从机场起飞后,就沿与原来的飞行方向成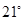 角的方向飞行,飞行到中途,再沿与原来的飞行方向成
角的方向飞行,飞行到中途,再沿与原来的飞行方向成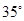 夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?
夹角的方向继续飞行直到终点.这样飞机的飞行路程比原来路程700km远了多少?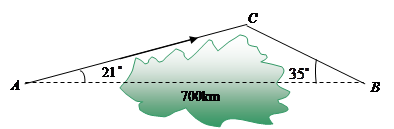
一架飞机在海拔8000m的高度飞行,在空中测出前下方海岛两侧海岸俯角分别是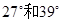 ,计算这个海岛的宽度.
,计算这个海岛的宽度.
如图,已知一艘船从30 n mile/h的速度往北偏东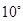 的A岛行驶,计划到达A岛后停留10 min后继续驶往B岛,B岛在A岛的北偏西
的A岛行驶,计划到达A岛后停留10 min后继续驶往B岛,B岛在A岛的北偏西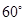 的方向上.船到达C处时是上午10时整,此时测得B岛在北偏西
的方向上.船到达C处时是上午10时整,此时测得B岛在北偏西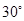 的方向,经过20 min到达D处,测得B岛在北偏西
的方向,经过20 min到达D处,测得B岛在北偏西 的方向,如果一切正常的话,此船何时能到达B岛?
的方向,如果一切正常的话,此船何时能到达B岛?
轮船A和轮船B在中午12时离开海港C,两艘轮船的航行方向之间的夹角为 ,轮船A的航行速度是25 n mile/h,轮船B的航行速度是15 n mile/h,下午2时两船之间的距离是多少?
,轮船A的航行速度是25 n mile/h,轮船B的航行速度是15 n mile/h,下午2时两船之间的距离是多少?
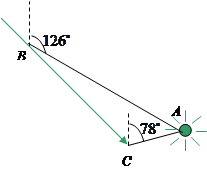
如图,货轮在海上以35n mile / h的速度沿着方位角(从指北方向顺时针转到目标方向线的水平角)为 的方向航行.为了确定船位,在B点观察灯塔A的方位角是
的方向航行.为了确定船位,在B点观察灯塔A的方位角是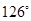 ,航行半小时后到达C点,观察灯塔A的方位角是
,航行半小时后到达C点,观察灯塔A的方位角是 .求货轮到达C点时与灯塔A的距离(精确到1 n mile).
.求货轮到达C点时与灯塔A的距离(精确到1 n mile).