某超市在节日期间进行有奖促销,凡在该超市购物满300元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球.顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就要将奖盒中的球全部摸出才停止.规定摸到红球奖励10元,摸到白球或黄球奖励5元,摸到黑球不奖励.
(Ⅰ)求1名顾客摸球3次停止摸奖的概率;
(Ⅱ)记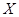 为1名顾客摸奖获得的奖金数额,求随机变量
为1名顾客摸奖获得的奖金数额,求随机变量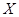 的分布列和数学期望.
的分布列和数学期望.
已知向量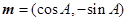 ,
,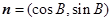 ,
,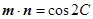 ,其中
,其中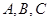 为
为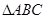 的内角.
的内角.
(Ⅰ)求角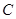 的大小;
的大小;
(Ⅱ)若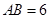 ,且
,且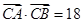 ,求
,求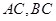 的长.
的长.
设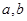 为实数,我们称
为实数,我们称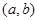 为有序实数对.类似地,设
为有序实数对.类似地,设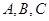 为集合,我们称
为集合,我们称 为有序三元组.如果集合
为有序三元组.如果集合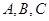 满足
满足 ,且
,且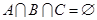 ,则我们称有序三元组
,则我们称有序三元组 为最小相交(
为最小相交(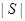 表示集合
表示集合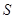 中的元素的个数).
中的元素的个数).
(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合 的子集构成的所有有序三元组中,令
的子集构成的所有有序三元组中,令 为最小相交的有序三元组的个数,求
为最小相交的有序三元组的个数,求 的值.
的值.
在平面直角坐标系 中,已知曲线
中,已知曲线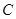 上任意一点到点
上任意一点到点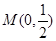 的距离与到直线
的距离与到直线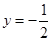 的距离相等.
的距离相等.
(Ⅰ)求曲线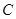 的方程;
的方程;
(Ⅱ)设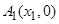 ,
, 是
是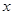 轴上的两点
轴上的两点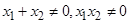 ,过点
,过点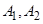 分别作
分别作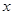 轴的垂线,与曲线
轴的垂线,与曲线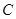 分别交于点
分别交于点 ,直线
,直线 与x轴交于点
与x轴交于点 ,这样就称
,这样就称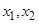 确定了
确定了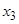 .同样,可由
.同样,可由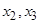 确定了
确定了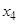 .现已知
.现已知 ,求
,求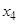 的值.
的值.
设实数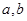 满足
满足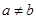 ,求证:
,求证: .
.
已知曲线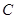 的极坐标方程为
的极坐标方程为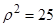 ,曲线
,曲线 的极坐标方程为
的极坐标方程为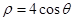 .试求曲线
.试求曲线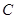 和
和 的直角坐标方程,并判断两曲线的位置关系.
的直角坐标方程,并判断两曲线的位置关系.