设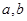 为实数,我们称
为实数,我们称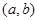 为有序实数对.类似地,设
为有序实数对.类似地,设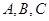 为集合,我们称
为集合,我们称 为有序三元组.如果集合
为有序三元组.如果集合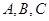 满足
满足 ,且
,且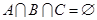 ,则我们称有序三元组
,则我们称有序三元组 为最小相交(
为最小相交(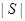 表示集合
表示集合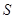 中的元素的个数).
中的元素的个数).
(Ⅰ)请写出一个最小相交的有序三元组,并说明理由;
(Ⅱ)由集合 的子集构成的所有有序三元组中,令
的子集构成的所有有序三元组中,令 为最小相交的有序三元组的个数,求
为最小相交的有序三元组的个数,求 的值.
的值.
(本题满分14分)已知椭圆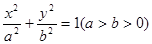 的离心率为
的离心率为 ,点P(1,
,点P(1, )在该椭圆上.
)在该椭圆上.
(1)求椭圆的标准方程;
(2)若直线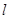 与圆O:
与圆O: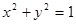 相切,并椭圆交于不同的两点A、B,求
相切,并椭圆交于不同的两点A、B,求
△AOB面积S的最大值.
(本题满分13分)已知函数 ,
, (a、b为常数).
(a、b为常数).
(1)求函数 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)当函数g(x)在x=2处取得极值-2.求函数 的解析式;
的解析式;
(3)当 时,设
时,设 ,若函数
,若函数 在定义域上存在单调减区间,求实数b的取值范围;
在定义域上存在单调减区间,求实数b的取值范围;
(本题满分12分)已知函数f(x)=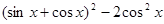 (
(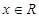 ).
).
(1)求函数f(x)的周期和递增区间;
(2)若函数 在[0,
在[0,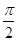 ]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
]上有两个不同的零点x1、x2,求tan(x1+x2)的值.
(本题满分12分)如图所示,在正方体ABCD—A1B1C1D1中, E、F分别是棱DD1、C1D1的中点.
(1)求直线BE和平面ABB1A1所成角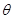 的正弦值;
的正弦值;
(2)证明:B1F∥平面A1BE.
(本题满分12分)某种有奖销售的小食品,袋内印有“免费赠送一袋”或“谢谢品尝”字样,购买一袋若其袋内印有“免费赠送一袋”字样即为中奖,中奖概率为 .甲、乙、丙三位同学每人购买了一袋该食品。
.甲、乙、丙三位同学每人购买了一袋该食品。
(1)求三位同学都没有中奖的概率;
(2)求三位同学中至少有两位没有中奖的概率.