(本题满分13分)已知函数 ,
, (a、b为常数).
(a、b为常数).
(1)求函数 在点(1,
在点(1, )处的切线方程;
)处的切线方程;
(2)当函数g(x)在x=2处取得极值-2.求函数 的解析式;
的解析式;
(3)当 时,设
时,设 ,若函数
,若函数 在定义域上存在单调减区间,求实数b的取值范围;
在定义域上存在单调减区间,求实数b的取值范围;
甲、乙两人进行乒乓球单打比赛,比赛规则为:七局四胜制,每场比赛均不出现平局.假设两人在每场比赛中获胜的概率都为 .
.
(1) 求需要比赛场数 的分布列及数学期望
的分布列及数学期望 ;
;
(2) 如果比赛场馆是租借的,场地租金 元,而且每赛一场追加服务费
元,而且每赛一场追加服务费 元,那么举行一次这样的比赛,预计平均花费多少元?
元,那么举行一次这样的比赛,预计平均花费多少元?
已知 为实数,证明:
为实数,证明: .
.
已知函数 ,
,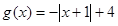 .
.
(1)若函数 的值不大于
的值不大于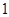 ,求
,求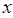 的取值范围;
的取值范围;
(2)若不等式 的解集为
的解集为 ,求
,求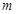 的取值范围.
的取值范围.
在直角坐标系 内,直线
内,直线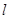 的参数方程
的参数方程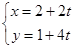 (
(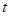 为参数),以
为参数),以 为极轴建立极坐标系,圆
为极轴建立极坐标系,圆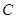 的极坐标方程为
的极坐标方程为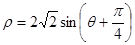 .
.
(1)求直线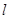 的普通方程和圆
的普通方程和圆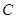 的直角坐标方程;
的直角坐标方程;
(2)确定直线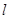 和圆
和圆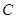 的位置关系.
的位置关系.
在直角坐标系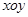 中,点
中,点 在矩阵
在矩阵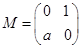 对应变换作用下得到点
对应变换作用下得到点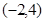 ,曲线
,曲线 在矩阵
在矩阵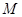 对应变换作用下得到曲线
对应变换作用下得到曲线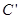 ,求曲线
,求曲线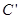 的方程.
的方程.