（本小题满分8分）已知盒中装有仅颜色不同的玻璃球6个，其中红球2个、
黑球3个、白球1个.
（1）从中任取1个球, 求取得红球或黑球的概率；
（2）列出一次任取2个球的所有基本事件；
（3）从中取2个球，求至少有一个红球的概率.
（本小题满分10分）
已知集合A＝{x|2－a≤x≤2＋a}，B＝{x|x≤1或x≥4}．
（1）当a＝3时，求A∩B；
（2）若A∩B＝Ø，求实数a的取值范围．
已知集合A=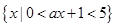
，集合B=
若A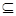
B，求实数a的取值范围；
设集合A＝{1，－2，a2－1}，B＝{1，a2－3a,0}．且A＝B，
（1）求a的值．
（2）判断函数f（x）＝x+
在[1，＋∞）的单调性，并用定义加以证明．
设定义在[－2,2]上的奇函数f（x）在区间[0,2]上单调递减，若f（m）＋f（m－1）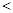
0，求实数m的取值范围．
如图所示，折线是某电信局规定打长途电话所需要付的电话费y（元）与通话时间t（分钟）之间的函数关系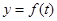
的图象，根据图象回答下列问题：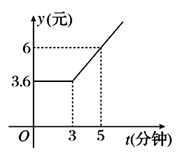
（1）求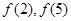
的值；
（2）求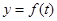的解析式及其值域。