在极坐标系中,已知圆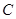 的圆心
的圆心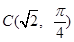 ,半径
,半径 .
.
(Ⅰ)求圆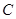 的极坐标方程;
的极坐标方程;
(Ⅱ)若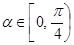 ,直线
,直线 的参数方程为
的参数方程为 (
(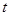 为参数),直线
为参数),直线 交圆
交圆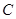 于
于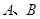 两点,求弦长
两点,求弦长 的取值范围.
的取值范围.
(本小题满分16分)如图,正四棱锥P-ABCD中,O是底面正方形的中心,E是PC的中点,求证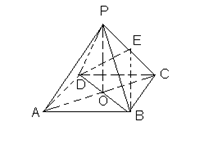
(1)PA∥平面BDE
(2)平面PAC  平面BDE
平面BDE
(本小题满分12分)有4名老师和4名学生站成一排照相。
(I)4名学生必须排在一起,共有多少种不同的排法?
(II)任两名学生都不能相邻,共有多少种不同的排法?
(III)老师和学生相间排列,共有多少种不同的排法?(要求用数字作答)
(本小题共10分)在直三棱柱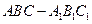 中,
中, ,
, ,求
,求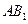 与侧面
与侧面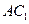 所成的角。
所成的角。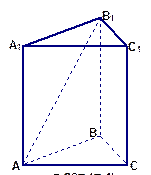
设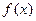 是定义在实数
是定义在实数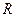 上的函数,
上的函数,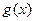 是定义在正整数
是定义在正整数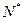 上的函数,同时满足下列条件:
上的函数,同时满足下列条件:
(1)任意 ,有
,有 ,当
,当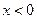 时,
时,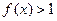 且
且 ;
;
(2)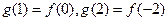 ;
;
(3)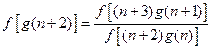 ,
,
试求:(1)证明:任意 ,
,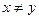 ,都有
,都有 ;
;
(2)是否存在正整数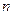 ,使得
,使得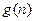 是25的倍数,若存在,求出所有自然数
是25的倍数,若存在,求出所有自然数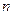 ;若不存在说明理由.(阶乘定义:
;若不存在说明理由.(阶乘定义: )
)
已知正实数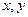 ,设
,设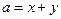 ,
,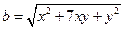 .
.
(1)当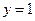 时,求
时,求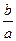 的取值范围;
的取值范围;
(2)若以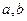 为三角形的两边,第三条边长为
为三角形的两边,第三条边长为 构成三角形,求
构成三角形,求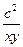 的取值范围.
的取值范围.