设函数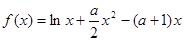 (
(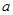 为常数)
为常数)
(Ⅰ)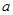 =2时,求
=2时,求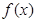 的单调区间;
的单调区间;
(Ⅱ)当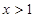 时,
时,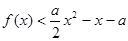 ,求
,求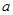 的取值范围
的取值范围
已知函数
(I)求函数 的最小正周期;
的最小正周期;
(II)若函数 的图象按
的图象按 平移后得到函数
平移后得到函数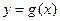 的图象,求
的图象,求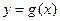 在
在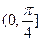 上的最大值.
上的最大值.
如图,在棱长为1的正方体ABCD—A1B1C1D1中,AC与BD交于点E,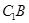 与
与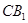 交于点F.(I)求证:
交于点F.(I)求证: ⊥
⊥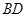 ;
;
(II)求二面角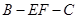 的大小(结果用反三角函数值表示).
的大小(结果用反三角函数值表示).
甲、乙、丙3人投篮,投进的概率分别是 ,
,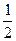 ,
, . 现3人各投篮1次,
. 现3人各投篮1次,
求:(Ⅰ)3人都投进的概率
(Ⅱ)3人中恰有2人投进的概率
设等差数列 的首项为
的首项为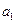 ,公差为
,公差为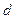 ,若
,若 ,
,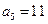 .
.
求:(1)数列的首项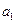 ,公差
,公差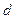 ;(2) 数列的通项公式
;(2) 数列的通项公式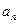
(本题满分15分)已知函数f(x)=(2-a)(x-1)-2lnx,,其中a∈R,
(1)求f(x)的单调区间;
(2)若函数f(x)在(0,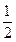 )上无零点,求a的取值范围.
)上无零点,求a的取值范围.