如图所示,有一范围足够大的匀强磁场,磁感应强度 ,磁场方向垂直纸面向里。在磁场中有一半径
,磁场方向垂直纸面向里。在磁场中有一半径 的金属圆环,磁场与圆环面垂直,圆环上分别接有灯
的金属圆环,磁场与圆环面垂直,圆环上分别接有灯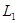 、
、 ,两灯的电阻均为
,两灯的电阻均为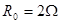 。一金属棒MN与圆环接触良好,棒与圆环的电阻均忽略不计。
。一金属棒MN与圆环接触良好,棒与圆环的电阻均忽略不计。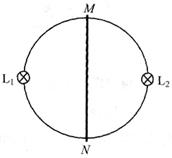
(1)若棒以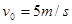 的速率在环上向右匀速滑动,求棒滑过圆环直径的瞬时MN中的电动势和流过灯
的速率在环上向右匀速滑动,求棒滑过圆环直径的瞬时MN中的电动势和流过灯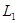 的电流;
的电流;
(2)撤去金属棒MN,若此时磁场随时间均匀变化,磁感应强度的变化率为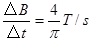 ,求回路中的电动势和灯
,求回路中的电动势和灯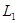 的电功率。
的电功率。
封闭在气缸内一定质量的理想气体由状态A变到状态D,其体积V与热力学温度关T系如图所示,该气体的摩尔质量为M,状态A的体积为V0,温度为T0,O、A、D三点在同一直线上,阿伏伽德罗常数为NA。
(1)由状态A变到状态D过程中 ▲
A.气体从外界吸收热量,内能增加
B.气体体积增大,单位时间内与器壁单位面积碰撞的分子数减少
C.气体温度升高,每个气体分子的动能都会增大
D.气体的密度不变
(2)在上述过程中,气体对外做功为5J,内能增加9J,则气体 ▲(选“吸收”或“放出”)热量▲J。
(3)在状态D,该气体的密度为ρ,体积为2V0,则状态D的温度为多少?该气体的分子数为多少?
质量m=1 kg的物体,在水平拉力F(拉力方向与物体初速度方向相同)的作用下,沿粗糙水平面运动,经过位移4 m时,拉力F停止作用,运动到位移是8 m时物体停止,运动过程中Ek-x的图线如图所示.求:(g取10 m/s2)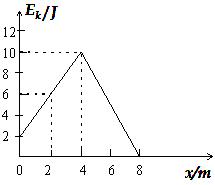
(1)物体的初速度多大?
(2)物体和平面间的动摩擦因数为多大?
(3)拉力F的大小.
如图所示,光滑斜面的长为L=1 m、高为H=0.6 m,质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连,开始时A物体离地高为h=0.5 m,B物体恰在斜面底端,静止起释放它们,B物体滑到斜面顶端时速度恰好减为零,求A、B两物体的质量比mA︰mB。
某同学解答如下:对A、B两物体的整个运动过程,由系统机械能守恒定律得mAgh―mBgH=0,可求得两物体的质量之比……。
你认为该同学的解答是否正确,如果正确,请解出最后结果;如果不正确,请说明理由,并作出正确解答。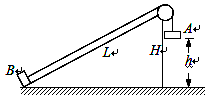
一辆质量为m、额定功率为P的汽车以额定功率在水平地面上匀速行驶,速度为v0.从某时刻起关闭发动机.试求
(1)汽车受到的平均阻力;
(2)汽车关闭发动机时的初动能;
(3)汽车关闭发动机后在水平地面上滑行的距离。
如图所示,在高为h=5m的平台右边缘上,放着一个质量M=3kg的铁块,现有一质量为m=lkg的钢球以v0=10m/s的水平速度与铁块在极短的时间内发生正碰被反弹,落地点距离平台右边缘的水平距离为I=2m.已知铁块与平台之间的动摩擦因数为0.5,求铁块在平台上滑行的距离s(不计空气阻力,铁块和钢球都看成质点,g=l0m/s2).