2011年8月韩国大邱世界田径锦标赛中的110米栏决赛中，在倒数第二个栏架和最后一个栏架，罗伯斯两次与刘翔发生了碰撞，最后一次还拉拽了刘翔的手，致使刘翔失去平衡，只排在第三位冲过终点，成绩是13秒27，已知110米栏是由110米的跑道和跑道上面的10个跨栏组成的。男子110米栏栏架高度 1.067米，第一栏距起跑线13.72米。栏间距 9.14米，最后一个栏架距终点线的距离 14.02米 。研究人员对刘翔110米栏全过程进行了研究分析，情况比较复杂，在这里，我们把全过程分为三个直线运动阶段，第一个阶段：从起跑到跑到第一个栏时，速度由零增加到全程运动中的最大速度为9.53m/s，近似认为是匀加速运动；第二阶段：一般认为匀速运动，从第一个栏到第十个栏的时间为8.79s，但是由于罗伯斯干扰，跨过第十个栏时的瞬时速度发生突变，第三阶段：最后的冲刺阶段，以跨过第十个栏时的速度开始匀加速运动，直到以全程的最大速度冲过终点，
（1） 求第一阶段所用时间为多少？
（2） 求第三阶段的加速度和跨过第十个栏时的速度为多少？
（所有结果都保留三位有效数字）
如图所示，质量为m=50g，长l=10cm的铜棒，用长度相等的两根轻软导线悬吊在竖直向上的匀强磁场中，导线跟铜棒的接触良好，磁感应强度B=0.5T。当导线中通入某恒定电流后，铜棒恰好偏离竖直方向37°而静止。求：铜棒中所通恒定电流的大小和方向。（g=10m/s2）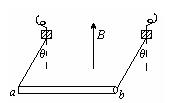
水平固定的两个足够长的平行光滑杆MN、PQ，两者之间的间距为L，两光滑杆上分别穿有一个质量分别为MA=0.1kg和MB=0.2kg的小球A、B，两小球之间用一根自然长度也为L的轻质橡皮绳相连接，开始时两小球处于静止状态，如图（a）所示。现给小球A一沿杆向右的水平速度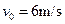
，以向右为速度正方向，以小球A获得速度开始计时得到A球的v-t图象如图(b)所示。（以后的运动中橡皮绳的伸长均不超过其弹性限度。）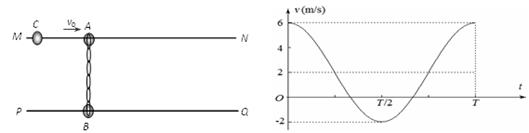
（1）在图(b)中画出一个周期内B球的v-t图象（不需要推导过程）；
（2）若在A球的左侧较远处还有另一质量为MC=0.1kg粘性小球C，当它遇到小球A，即能与之结合在一起。某一时刻开始C球以4m/s的速度向右匀速运动，在A的速度为向右大小为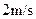
时，C遇到小球A，则此后橡皮绳的最大弹性势能为多少？
（3）C球仍以4m/s的速度向右匀速运动，试定量分析在C与Ａ相遇的各种可能情况下橡皮绳的最大弹性势能。
如图，长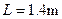
，高h=1.25m，质量M=30kg的小车在水平路面上行驶，车与路面的动摩擦因数
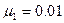，当速度
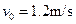时，把一质量为m=20kg的铁块轻轻地放在车的前端（铁块视为质点），铁块与车上板间动摩擦因数
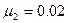，问：（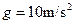
）
(1) 铁块与小车分离时铁块和小车的速度分别为多少？
(2) 铁块着地时距车的尾端多远？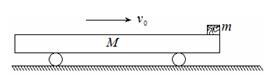
有一质量为m的航天器靠近地球表面绕地球作匀速圆周运动（轨道半径等于地球半径），某时刻航天器启动发动机，向后喷气，在很短的时间内动能变为原来的
，此后轨道变为椭圆，远地点与近地点距地心的距离之比是2：1，经过远地点和经过近地点的速度之比为1：2。己知地球半径为R，地球表面重力加速度为g。
（1）求航天器在靠近地球表面绕地球作圆周运动时的周期T；
（2）求航天器靠近地球表面绕地球作圆周运动时的动能；
（3）在从近地点运动到远地点的过程中克服地球引力所做的功为多少?
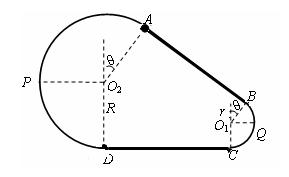
如图所示为放置在竖直平面内游戏滑轨的模拟装置，滑轨由四部分粗细均匀的金属杆组成，其中倾斜直轨AB与水平直轨CD长均为L＝3m，圆弧形轨道APD和BQC均光滑，BQC的半径为r＝1m，APD的半径为R=2m，AB、CD与两圆弧形轨道相切，O2A、O1B与竖直方向的夹角均为q＝37°。现有一质量为m＝1kg的小球穿在滑轨上，以Ek0的初动能从B点开始沿AB向上运动，小球与两段直轨道间的动摩擦因数均为μ＝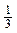
，设小球经过轨道连接处均无能量损失。（g＝10m/s2，sin37°＝0.6，cos37°＝0.8），求：
（1）要使小球完成一周运动回到B点，初动能EK0至少多大？
（2）若以题（1）中求得的最小初动能EK0从B点向上运动，求小球第二次到达D点时的动能；
（3）若以题（1）中求得的最小初动能EK0从B点向上运动，求小球在CD段上运动的总路程。